The Multi-Wave Skew-Logistic Process Applied to the UK COVID-19 Pandemic and being Carbon Negative in Climate Change
Article Information
Dr. Russell Cheng1*, Dr. Brian Williams2
1University of Southampton, Highfield, SO17 5BJ, United Kingdom
2SACEMA, Stellenbosch University, South Africa
*Corresponding author: Dr. Russell Cheng, University of Southampton, Highfield, SO17 5BJ, United Kingdom.
Received: 24 June 2024; Accepted: 01 July 2024; Published: 13 July 2024
Citation: Dr. Russell Cheng, Dr. Brian Williams. The Multi-Wave Skew-Logistic Process Applied to the UK COVID-19 Pandemic and being Carbon Negative in Climate Change. Archives of Clinical and Biomedical Research. 8 (2024): 301-316.
View / Download Pdf Share at FacebookAbstract
The Skew-Logistic (SL) function has been proposed to model a reallife dynamic process which rises monotonically to a peak followed by a monotonic falling back. It was introduced to model the first stage of the COVID-19 pandemic in order to forecast its behaviour. Then, with different controls and variants, COVID-19 rose and fell in what might be called a Multi-Wave (MW) behaviour with waves not necessarily the same size. This paper shows how using the Skew Logistic (SL) function for one wave can be modified to model the MW situation. We apply it to two examples. One is to COVID-19 in order to show its more recent behaviour, the other is to climate change, the most serious issue of our time. Some background is provided for both application problems.
Keywords
COVID-19 waves; Climate change; Carbon negative
COVID-19 waves articles; Climate change articles; Carbon negative articles
Article Details
1. Introduction
The SL function was introduced in [11] to compare the first wave of the COVID-19 epidemics in European countries. The mathematical form is described in the Supplementary Materials of that paper which also describes how the model can be fitted to real data using standard statistical techniques.
This paper shows how the method can not only be used to fit it to individual waves, but can also be first fitted to the separate waves of a Multi-Wave (MW) data sample, that can then be combined to create an overall fit to the entire data sample. See also [8] and [9]. In Section 2 the SL Function is defined and Single wave fitting is summarized. Then, in Section 3, we discuss the MW fitting method. The present paper is based on Cheng and Williams [7].
In this article we give two examples of fitting the SL Multi-Wave model to a data sample.
The first example comprises more recent COVID-19 UK Daily Active Cases up to February 2023 covering 3 waves. The pandemic in the UK is essentially over. But as COVID-19 is now endemic, there will of course be many more minor waves, every year. However basically the risk is now understood and we are back to normal.
As a second example, we fit the SL-MW model to the average global annual atmospheric carbon dioxide level in parts per million (CO2 ppm) from 1800 to 2022/4 and to the world average global annual atmospheric temperature. We use the fits to predict the CO2 and temperature levels until 2100 to show what would happen if human behaviour does not change.
All predictive models depend on underlying assumptions. Both examples involve problems that involve innumerable factors; so our model might be considered over simplistic. However as observed by Box (1976): ‘All models are wrong, but some are useful.’
Even though many factors may be involved, sometimes just one factor encapsulates the whole process. For the COVID-19 example [16] show that, in a whole population, the proportion of susceptibles not contracting the virus depends exponentially (commonly denoted in logarithmic form) only on R0, the reproduction number. And in the CO2 example the second Arrhenius equation shows how atmospheric temperature depends exponentially on atmospheric CO2 involving only one parameter, commonly denoted by α. Many natural processes are exponential/logarithmic, and in this sense our SL Multi-Wave model is well suited to both examples.
Section 4 describes the SL-Fitting method for both examples. This uses the bootstrapping method, (See Cheng, 2017, for example) to construct a confidence band (CB) with a probability greater than or equal to (1 - α) of containing the SL function trajectory within the upper and lower loci of the CB, with selected by the user. Note that a confidence band (CB) is different from a (simultaneous) confidence interval (CI), with the entire trajectory of the fitted curve within the upper and lower loci of the band with confidence level of at least that which has been set. In the earlier cited work, CB’s were used to forecast how the one-wave epidemic was likely to behave [3] [4] [6].
Section 5 discusses error estimation and how it is applied in both examples. Sections 6 and 7 discuss the implicaton of the results in each example with an overall Summary in Section 8.
Appendix A, for convenience, summarizes the COV-19 model as described in the Supplementary Materials of Dye et al. (2020), and also comments on the contribution in Levene (2022). Appendix B summarizes the CO2 model highlighting the work of Arrhenius (1896). Appendix C considers two possible different models.
Overall, the aim of our paper is to describe how to extend SL Fitting of One-Wave to Multi-Wave situations and to apply this to two important current problems.
2. Single waves
2.1 The Statistical form for a Data Sample
We assume that the process which we are investigating is a function F(t,θ) depending on time t and a vector of parameters θ. We can study the trajectory of this process over a given period of time; obtaining a sample of n+1 observations of the process over n equally spaced time steps
{F(ti, θ): i = 0, 1,…, n}, where t0 = 0 and tn = T = nh, say, and h is the step length.
We suppose that F(t,θ) is differentiable, satisfying the ordinary differential equation

If T is fixed, and h is small and observed with small error, then it is well approximated by step by step Euler numerical integration of the recursive equation:

2.2 The SL Function
We examine the form of when it is an SL Function. As described in [12] this takes either of two equivalent forms:

where D(t,θ) is the prevalence or incidence of the quantity of interest, this being the number of daily cases of COVID-19 in the UK in Example 1 and the global average concentration of CO2 concentration in parts per million (ppm) in Example 2. All four parameters are readily interpretable. The parameter a, is close to the maximum value of D(t, θ), while τ indicates the location of the maximum. The parameters b and d, respectively, indicate the rates of rise and decline of D(t, θ). As shown in Equation 1, b and d are mathematically equivalent.
We write θ=(σ,a,b,τ)where σ is the standard deviation of an individual observation. As the dependence of D(t, θ) on the parameters is obvious, θ is usually but not invariably, omitted. We assume that b > 0 and d < 0 so that the term (b-d)/2 in the denominator is always positive. D(t)≅ eb(t-τ) when t →-∞, so that b gives the exponential rate of increase of D(t) as t increases from -∞ and D(t)≅ ed(t-τ) when t →∞, so that d < 0 gives the exponential rate of decrease. Either form of D(t)in Equation 1 can be used when fitting to data, with the signs of b and d showing which role they have.
The explicit maximum value of D(t) is:

where r=-b/d. The maximum occurs at

Equations (2) and (3) show that, when b and are close in value, will be close to the maximum of D, and will be close to the position of the maximum.
2.3 Fitting the SL Function to one Wave
As mentioned in the Introduction, fitting the SL function to the observations of one wave of the process of interest is fully described in the Supplementary Materials of [11]. For convenience the fitting process is summarized in Appendix A here.
We fit the SL function to data using the method of maximum likelihood (ML) and a Nelder-Mead search [23]. An advantage of Nelder-Mead is that computational complexity depends linearly on the number of parameters, say m; and not on m2 as with gradient methods.
A very attractive feature of the SL function, as parameterized in [12], is that all the parameters, unlike that used in [17], are readily and separately interpretable. This enables the user to visually select appropriate initial values as required by Nelder-Mead search. An initial value for a can be obtained using Equation (2) for the wave height, an initial value of using Equation (3) can be used for the wave location. The rates of increase and decrease of the wave can each be interactively estimated to give starting values for b and d. There is of course some intercraction between the steps. But little practice is needed to master the method.
An important watch point is that the SL function, when it decays, tends to zero. So long as the process is known to have a minimum this can allowed for, or included in the estimation process. In our two examples the base line is already known and does not need estimation.
In applying ML optimization, we include an extra parameter σ, the standard deviation of the observational error. Estimation of σ is included in the ML method, so that the quality of the fit is also assessed.
3. Multi-Wave DATA
3.1 Function Formula and Data Examples
When there are N waves, we assume a simple, additive functional form, namely:

where θcomprises all the parameters σ, {ai,bi,di,τi}(i=1,2,...,N) and typically, but not invariably, the τi are in increasing order τ1<τ2...<τN indicating the approximate location of each of the maxima of the waves. We give two data samples where D(t,θ) can be fitted.
The first, Example 1, comprises the observed Daily Active Cases of COVID-19 from 17 March 2022 to 3 November 2022 as shown in Figure 1.
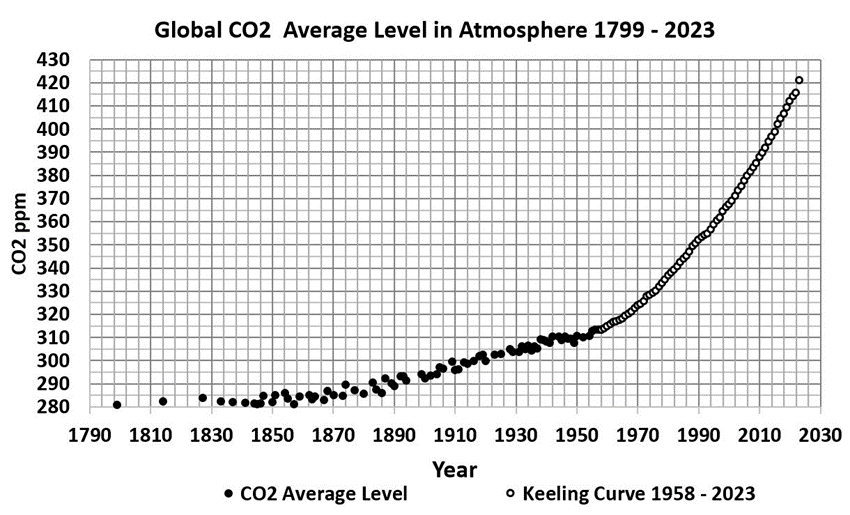
Example 2, comprises the observations of the global CO2 level, in parts per million (CO2 ppm), from 1799 to 2023 as shown in Figure 2.
are the Mauna Loa observations made mainly by C. D. Keeling of the Scripps Institution of
Oceanography, Global Monitoring Laboratory, National Oceanic & Atmospheric Administration (GML NOAA). See [15].
When a wave is particularly prominent, there is a noticeable peak in a data sample plot, but this depends on the juxtaposition of the waves so that where a wave peaks may not be obvious from the full sample plot. In Example 1, one might conjecture that there are three waves. In Example 2, it is less clear if there are one or two waves.
3.2 The Basic Fitting Method
The proposed method of fitting D(t) to data takes two stages. The first stage is key where the data are grouped into separate sections, with each representing the position where the data are most dependent on one particular wave. The division process needs to be made automatic, as required with a very fast real-time process as in a digital twin simulation, see [18] for example. But if instant speed is not important and this is the case in our two examples, then it is simplest for the user to carry out this process by eye. As already mentioned, in Example 1, the number of waves looks likely to be three, whilst the choice is less obvious in Example 2. In the latter case the initial slope variation suggests an earlier wave that becomes dominated by a second wave. Here more adjustment is needed to fix the position of the first wave and our final choice turns out to be two waves.
With a choice of the number of waves and their likely positions made, a single wave model is separately fitted to each section of the data.There are four parameters, for each section so that in Example 1, with three waves fitted, the total number of parameters is 13 as we assume the same standard deviation for all waves. Varying is possible, but there was no evidence this was needed in this case. Similarly for Example 2 the total number of parameters in the full fit is 9.
In the second stage the MW model of Equation (4) is then fitted to the entire data set using, as the initial parameter estimates, the values obtained in the first stage for each of the single waves.
To find the maximum when using search methods like Nelder-Mead, a good choice of initial parameters is important, particularly when the parameter count is high and the search domain is high dimensional. The problem is particularly demanding when the function is multimodal. In our case, visual evidence of a good fit of a regression line to data, together with confidence level assessment, provides reassurance that our visual method is satisfactory. In the next section we study the Examples in more detail.
4. Fitting Method in Our Examples
4.1 COVID-19 Example
Our overall approach is to divide the fitting into two steps.
We first consider Example 1.
We start with a visual inspection of the sample. This suggests choosing 3 waves with waves 1,2 and 3 contributing respectively to data sets in the ranges S1 = {1, 86}, S2 = {87,172}, S3 = (173,243}, the sample size being n = 243. We then separately fit the single wave SL model of D(t), as given in Equation (1), to each of the data sets Sj, j = 1,2,3. The fitting process is described in [8] and in [11], Supplementary Materials, and will not be repeated here. Figure 3 gives the results of this step.
The easy selection of likely parameter values, based on the shape and location of data sub-samples, allows charting tools to be developed for obtaining a good initial fit. Such initial values provide a starting point for the Nelder-Mead optimization. Charting tools enable the sensitivity of the fit to changes in parameter values to be examined at any stage of the fitting process; though this is not really necessary, as bootstrapping provides more reliable quantified evidence of fit. The fitted parameter values are given in Table 1 below.
|
Parameters |
1-86: Wave 1 |
87-172 Wave 2 |
173-243 Wave 3 |
|
4490 |
1630 |
748 |
|
|
254000 |
101000 |
27500 |
|
|
0.215 |
0.103 |
0.0492 |
|
|
-0.0596 |
-0.0713 |
-0.174 |
|
|
44629 |
44741 |
4485 |
Table 1: Parameter estimates obtained by dividing the full sample into 3 subsamples and fitting a single wave separately to each subsample.
Once the single waves have been fitted, we proceed to the second step which is to fit the N=3, Multi-Wave D(t) of Equation (4) taking θ={σ,a1,b1,d1,τ1, a2,b2,d2,τ2, a3,b3,d3,τ3 as the vector of initial parameter values. The subscripts correspond to the number of the fitted wave.
The initial Multi-Wave D(t) obtained, using the initial parameter values of Table1, is shown in the chart of Figure 4. Fitting a wave to each separate data sample gives good separate individual fits but may not guarantee a good combined fit. In the present case the fit is very good with the final fit almost the same as the initial fit obtained by combining the parameters of the three single wave fits. The optimized parameter estimates are shown in Table 2.
|
Parameters |
i = 1 |
i = 2 |
i = 3 |
|
4610 |
|||
|
27000 |
102000 |
28300 |
|
|
0.198 |
0.0817 |
0.0483 |
|
|
-0.0637 |
-0.0874 |
-0.135 |
|
|
44630 |
44747 |
44852 |
Table 2: Parameter estimates obtained by an N=3 Multi-Wave fit to the full COVID-19 sample
4.2 CO2 Example
Visual inspection of the data sample of Figure 2 suggests fitting two waves in Figure 5. Because the SL wave rises from and then usually falls to zero, we have subtracted 280 ppm from the CO2 observations, so that the lowest value is just above zero. This allows D(t) to achieve a good fit. This value could be treated as an unknown parameter, but given that this limit is little changed over the years,little would be gained in estimating it. It might be thought that one wave might be sufficient. However, as Figure 5 shows, two waves are needed. The attraction of the SL function with parameters as defined, is that waves can be easily added or removed, and the result compared.
Figure 5: The two Single Wave fits for the (CO2 -280)ppm sub-samples: S1=1-76, S2=77-145. Using a Single Wave fit for the full sample gives a reasonable fit for the period of the sample observations. However there is a butterfly effect in which very different behaviour is obtained very much later, as the lower chart shows.
|
Parameters |
1-76: Wave 1 |
77-145 Wave 2 |
|
1.46 |
8.66 |
|
|
111.0 |
675 |
|
|
0.0394 |
0.0269 |
|
|
-0.0196 |
-0.784 |
|
|
1939.0 |
2078.0 |
Table 3: Parameter estimates obtained by dividing full Global CO2 sample into 2 subsamples and fitting a single wave separately to each subsample.
Use of these single wave parameter estimates as initial values produces the N=2 Multi-Wave fit shown in Figure 8 below. But before discussing Figure 8, we first discuss the temperature calculation.
4.3 Temperature Calculation
In this subsection we explain the calculation of the temperature curve from 1800 to 2022 plotted in Figure 8.
We see in the chart of Figure 6 that the Temperature Anomaly and CO2 concentration go up and down together.
We therefore plot, in Figure 7, the average global temperature against the Global CO2 concentration level. The chart indicates a general linear relationship in the data
We therefore make the simple first order linear assumption that T(t), the average global temperature in degrees centigrade is:

From 1800 to 2022, C(t), the global concentration level increased by about 48% from 280 ppm to 420 ppm, an increase of 140 ppm, whilst T(t) increased by about 1.5 degrees to the present 13.9 degrees. We can set as the initial base value of T(1800) = 0, so that from Equation 5, we have

The actual plot replaces C(t) by . Jonas (2015) derives a formula showing the yearly change in CO2 in terms of the corresponding change of year:
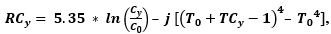
where RCy is the net downward infra-red radiation, IR, in the year y. It will be seen in Figure 8 that the calculation gives a good representation of the temperature up to the present; a comparable result to the SL fit. The difference of the curve based on Equation (5) and the other fits arises from different base T values used as the initial year. Figure 8 presents the results of the temperature calculations together with the CO2 ftting results
Figure 8: The N=2 Multi-Wave fit to the full Global CO2 ppm sample and the corresponding estimate of the Temperature using a linear approximation with D(t,θ) the mantissa, estimated by the SL method, see Subsection 4.3. Also shown are the fits obtained, by the Jonas calculation (the most optimistic) and the Denning (2015) estimate. The single point is the global average temperature in 2023.
5. Error estimation
5.1 Bootstrap Analysis
We calculate, numerically, confidence levels for D(t) by generating a parametric bootstrap samples, E(ti ) i= 1,2,…,n, each of the form:

is a random sample of mutually independent distributed, normal pseudorandom variables with variance σ2. We generate B bootstrap samples, so that we have

A confidence region for the parameters is then calculated from which confidence bands for the trajectories are obtained .
Regarding the sampling errors in the sample data, we could have used the simpler assumption that observational errors are independent, but instead we made a modification to model the dependence of an observation on previous observations. Specifically the observations are assumed to be a first order autoregressive process. Thus we set
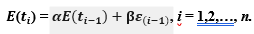
The standard deviation of an observation is therefore not , but is s, which is approximately

Thus values of α=0.75, β=0.25 would make s=σ.
The reliability of results is measured by just one parameter, σ. Our data samples are far too small to fully examine the accuracy of the estimate of σ. In practice, much larger data samples are required, however we could still simply vary the value of σ using the same MLEs of the SL parameters in our bootstrapping to assess how the CBs of the trajectories change, relying on the well-known property that the estimate of σ is asymptotically independent of the estimates of the other parameters (see Cheng, 2017, for example).
5.2 COVID-19 Bootstrap Results
Figure 9 shows scatterplots of the results of fitting the SL model for Wave 2 of the COVID-19 sample. Each scatterplot displays a white dot of the ML estimates of a pair of paraameters together with the corresponding B=250 bootstrapped ML estimates.
Figure 9: Scatterplots of MLEs of parameter pairs obtained by fitting the SL model to Wave 2 of the COVID-19 data sample, and the corresponding B =250 bootstrap MLEs. Bootstrapping the full 3-Wave MLE, when there are then 78 parameters, can be used to calculate a (1- α)% confidence band for unknown true sample trajectory.
Figure 10 gives shows the resulting D(t) plots of the MLE and the Upper and Lower CB curves with confidence level 90%.
5.3 CO2 Bootstrap Results
As with Figure 9, Figure 11 illustrates the results of fitting the SL model, only here for Wave 1 of the CO2 sample. Each chart displays a white dot of the ML estimates of a pair of parameters, together with the corresponding B =250 bootstrapped ML estimates.
Figure 11: The complete set of ten scatterplots for fitting one Wave in the CO2 Example. Note the high correlation of the b/d and a/tau scatterplots Note also the hyperbolic nature of a and tau each with b and d illustrating the property where bootstrapping can capture higher order correlations than classic asymptotic theory which only evaluates linear correlation.
For the upper and lower CB loci to be as narrow as possible and to ensure the selected confidence level is met, the loglikelihood used to construct the confidence should be convex. An attraction of bootstrapping is that though the confidence regions are not all convex so the CB may not be the narrowest possible, selection of the correct proportion of scatterpoints ensures the correct confidence level will be met.
Though not shown because of the number of scatterplots, we have examined the plots for the full Multi-Wave fits. For the COVID-19 case, all 78 plots are elliptic and for the CO2 case the 5 scatterplot regions are slightly parabolic, the remaining 73 elliptic. In both cases, the MLE of σ is smaller than all the bootstrapped values. This is may be preferable, erring on the side of caution., though of course could increase processing costs. Something that could be investigated in another paper.
Figure 12 shows the bootstrapping bands for both Global Mean Atmospheric CO2 and Temperature.
6. IMPLICATIONS OF COVID-19 SCENARIO
The COVID-19 pandemic is now effectively over in the UK. Permanent vigilance is needed and being applied as it is now endemic. Figure 13 below shows that COVID-19 is now in control in the UK.
When the epidemic is over, there is an interesting relationship between the number of people, called the susceptibles, who are initially uninfected, labelled , and those who survive the epidemic without ever becoming infected, labelled are in a final size relation found by Kermack and McKendrick [16], for the SIR model, who showed that in a population of size N:

Here the reproduction number is the number of susceptible individuals an infected person goes on to infect when the epidemic first starts, assuming the population is homogeneously mixed. does not change during the whole course of the epidemic. Suppression of the epidemic using lockdowns and isolation only changes the effective reproduction number, . This latter reproduction number, was used by politicians and medical personnel to report how well suppression methods were working during the epidemic, with the reassurance that, when was less than , it indicated the effectiveness of control policies. However, if control policies were removed before the epidemic is over, then . would revert back to . Only vaccination would reduce permanently.
7. Implications of CO2 Scenario
7.1 The End of the World
The key is to appreciate how CO2 influences temperature. One might argue that it could be that temperature influences CO2. Though this might be true to some extent for fauna and flora, but it is clear that many processes, not influenced by temperature, generate CO2, notably when human processes of digging, making and growing occur, moreover some contribute to both CO2 and temperature increase. The chart in Figure 14 shows the fits and predictions for CO2 and temperature. The scale used shows clearly the change in CO2 level that will lead to a further increase in one degree.
The ever increasing effect of each increase in one degree is listed in Table 4 below. Table 4: Impact of 6 Degrees of Temperature Change [Adapted from Lynas (2015))

Many believe that the tipping point is already past. Once past, there is no return. The disastrous end can be seen in the largest continent of Alaska. It will simply disappear.
7.2 What has Happened
Since the industrial revolution the concentration of CO2 in the atmosphere is now about 415 ppm (Figure 8) as the result of burning fossil fuels, so that the weight of carbon has increased to 880 billion tons, or about twice the weight of carbon in plants. The consequence of this is that the earth’s atmosphere has already experienced an increase in average temperature of about 1.5 C (Figure 8) with the prospect that, if the concentration of CO2 continues to increase, following the current trend, the temperature could increase by 6°C above preindustrial levels which would be catastrophic for our survival. We therefore need to sequester CO2 on a massive scale.
Gates (2021) [13] notes that ‘we are currently adding fifty-one billion tons of greenhouse gases to the atmosphere every year. He lists how this happens in 5 ways, the first three by far the most important: (i) making things, (ii) generating electricity (iii) growing things (iv) travelling and (v) keeping warm and not cool. Gates (2021) [13] points out that to avoid a climate disaster, we have to get to zero using the tools we already have, like solar and wind while creating breakthrough technologies that can take us the rest of the way’. But even this ambitious goal may not be sufficient. For 800,000 years (Figure 15) the level of CO2 in the atmosphere averaged about 230 ppm going slowly up and down by about 40 ppm with a period of about 100,000 years. Since the industrial revolution it has increased to over 400 ppm and is rising fast. To get back to pre-industrial revolution levels of CO2 we need to be massively carbon negative as indicated in Figure 15 and even then it would take more than 100 years to reach the target.
8. Summary
The main purpose of this paper has been to illustrate how the SL function can be used to represent data with a Multi-Wave form; with the main geometric features of each wave easily related to the parameters of a single SL function. These single SL functions provide a good starting point to enable a Multi-Wave SL function to fitted to the full data sample. Our COVID-19 example is such a case. Though not discussed here, the SL parameters can be reparametrized with transformed parameters representing infection levels and transition rates between the compartments of a compartment model, See Cheng et al (2020). It would be of interest in further work to link the SL parameters in the CO2 example to parameters on which climate change depends.
References
- Arrhenius S (1896) On the Influence of Carbonic Acid in the Air the Temperature of the Ground Philosophical Magazine and Journal of Science Series 5 (41): April, 237-276.
- Box George E. P. Science and Statistics. JASA, 71 (1976): 791.
- Cheng C.H. Confidence bands for two-stage design problems, Technometrics, 29 (1987): 301-309.
- Cheng C.H., Evans, B.E. and Williams, J.E. Confidence band estimations for distribution used in probabilistic design. International Journal of Mechanical Sciences, 30 (1988): 835-845.
- Cheng R C H. Non-Standard Parametric Statistical Inference. Oxford University Press, Oxford (2017).
- Cheng R. C. H. and Williams B. G. Uses of the Skew-Logistic function for Multi-Wave functions (2022).
- Cheng, R, Dye, C, Dagpunar J and Williams, B (2020) Modelling Presymptomatic Infectiousness in COVID-19. medRxiv 11 (2020): 20224014;
- Russell Cheng, Christopher Dye, John Dagpunar & Brian Williams Modelling presymptomatic infectiousness in COVID-19, Journal of Simulation (2023).
- Denning, Scott. (2015) Emissions calculator from Denning Research Group at Colorado State University http://biocycle.atmos.colostate.edu/shiny/emissions/ using no emissions cuts, ie, “Business as usual”. (Downloaded 20/5/2015. Digitised using xyExtract v5.1 (2011) by Wilton P Silva)
- Dye, C. Cheng, R C H, Dagpunar, J S & Williams, B G (2020) The scale and dynamics of COVID-19 epidemics across Europe medRxiv (2020).
- Dye C, Cheng R C H, Dagpunar J and Williams B G. The scale and dynamics of COVID-19 epidemics across Europe. R. Soc. Open Sci. 7 (2020): 201726
- Gates, W. How to avoid a climate disaster: the solutions we have and the breakthroughs we need. New York : Doubleday (2021).
- Jonas, M. (2015) The Mathematics of Carbon Dioxide, Part 1.
- Keeling C D, Piper S C, Bacastow R B, Wahlen M. Whorf T P, Heimann M, and Meijer H A. (2001) Exchanges of atmospheric CO2 and 13CO2 with the terrestrial biosphere and oceans from 1978 to 2000 I. Global aspects, SIO Reference Series, No. 01-06, Scripps Institution of Oceanography, San Diego, 88 pages (2001).
- Kermack W O and McKendrick A G (1927). A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A 115: 700-721.
- Levene M (2022). A Skew Logistic Distribution for Modelling COVID-19 Waves and Its Evaluation using the Empirical Survival Jensen–Shannon Divergence. Entrop, 24 (5), 600;
- Lichtenstern I and Kerber F (2022) Data-based digital twin of an automatic guided vehicle system. http://informs-sim.org/wsc22papers/by_area.html#ptrack224
- Lynas, M. (2015) (and Narrator) https://www.youtube.com/watch?v=7T9IjSEqT74
- Ma, J., & Earn, D. J. D. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bulletin of Mathematical Biology, 68 (2006): 679-702.
- Ma J (2020). Estimating epidemic exponential growth rate and basic reproduction number. Infectious Disease Modelling 5 (2020): 129-141.
- NASA’s GRACE and GRACE Follow-On satellite projects (2021) https://climate.nasa.gov/climate_resources/265/video-antarctic-ice-mass-loss-2002-2020/
- Nelder J A and Mead R (1965). A simplex method for function minimization. Computer Journal, 7: 308-313.
- Wikipedia Antarctica (Accessed 2023) https://www.bas.ac.uk/data/our-data/publication/ice-cores-and-climate-change/
https://wattsupwiththat.com/2015/07/25/the-mathematics-of-carbon-dioxide-part-1/
Author Biographies
Russell Cheng retired from the University of Southampton in 2007 where he had been Head of the Operational Research Group, having held previous positions at Cardiff University and the University of Kent at Canterbury. https://www.southampton.ac.uk/maths/about/staff/rchc.page
Brian Williams is Senior Research Fellow at the South African Centre for Epidemiological Modelling and Analysis (SACEMA) having held the position of Epidemiologist at the World Health Organization from which he retired in 2008.
APPENDIX A
A1 The SEPIR Model
This paper uses the same model as the one in Cheng at al. (2023). Here we describe its features as a reminder of the form of the model.
The model assumes a homogeneously mixed population with five compartments representing those who are (i) susceptible, (ii) exposed but not infectious (iii) presymptomatically infected by someone already infected and infectious but without symptoms, (iv) infected by someone with symptoms, and (v) recovered, as shown in Figure A1.

Figure A1: The SEPIR model. The compartments denote those in the population that are Susceptible, Exposed, Presymptomatically Infected, Infected by someone with symptoms and Recovered.
The arrow going from S to E represents (i) those infected by someone in P, with transmission rate , and also (ii) those infected by someone in I, with transmission rate The three arrows going from E to P, P to I, and I to R represent, respectively, (a) those exposed becoming infectious but not displaying symptoms (transmission rate ), (b) those infectious then showing symptoms (transmisison rate ) and (c) those infectious who show symptoms who recover (transmission rate ). These latter three parameters are standard in compartmental models, see Ma (2020) for example. The reciprocal is the mean period someone spends in (compartment) E. Likewise the reciprocal is the mean period someone spends in P and is the mean period spent in I.
As the risk of death from COVID-19 was of special concern, we included a parameter, , the proportion of individuals who recover well, as opposed to dying. The population infection fatality rate, (IFR), is 1- An individual’s IFR is highly dependent upon age. We estimate this probability by dividing infectious individuals, all of whom are assumed to ‘recover’, into two compartments (i) those that recover well and (ii) those that die due to the virus, as illustrated Figure A2.

Figure A2: Adjustment of the SEIR model where R is divided into two compartments, R \ Z, those that recover and Z, those that die; where is the proportion that recover.
Also included are five further parameters t0, e0,N, σ and , all listed and defined in columns 1 and 2 of Table 1 of Cheng et al (2023).
The variables S, E, P, I and R are the number of individual in each compartment. These satisfy the ordinary differential equations (ODEs) that we numerically .integrate to obtain the trajectories of the variables.
Full details of the model and fitting method are given in Cheng et al. (2023).
A2 Levene’s SL Model
Levene (2022) has also studied COVID-19 using the same SL model as ours, but treated as a statistical distribution and also with parameters differently defined. The paper is interesting but the fits are clearly inferior to our fits so we have not therefore not explored Levene’s paper further.
APPENDIX B
B1 The Problem of Climate Change
Humans face an existential threat as climate change is occurring ever more rapidly. As pointed out by Maslin (2021), human activity emits about 9 Gigatonnes per year, whilst other activity produces only 2.6 2.3 = 0.3 Gigatonnes a year indicating how our present activity is harming our planet.
B2 The CO2 Model
Arrhenius (1896) was a pioneer in pointing out the effect on Global Atmospheric Temperature of Global Atmospheric Carbon Dioxide (called Carbonic Acid in the 19th Century. After nearly a hundred thousand hand calculations; as modern computer based simulation models were not at his disposal, he was able to propose a simple regression model that related Global Temperature to Carbon Dioxide (called Carbonic Acid in the 19th Century) namely:

where T is the average global temperature, K is the mean quantity of CO2 absorbing heat from the Sun’s ray and. is the absorption constant of the air for the heat that radiates from the earth’s surface, and the albedo of the earth’s crust is . Note that T is the dependent variable with regarded as a constant while and K are considered as independent where the variation of the latter is of particular interest. Full details of K are given in Arrhenius (1896).
A modern interpretation of Arrhenius’s approach is to use the Second Arrhenius Equation (see Aber, 2022 for example) This uses the exponential regression equation:

where C is the average global atmospheric carbon dioxide level, with C1> C0two different levels, and T is the average global atmospheric temperature, with T1 and T0 corresponding to C1 and C0.
This can be represented by just two compartments, depicting T and C both moving together at the same time as shown in Figure B1:

Figure B1: The dependence, by a single parameter, α, of the temperature T on CO2 level.
In modern times the Intergovernmental Panel on Climate Change (IPCC) uses a standard protocol describing the minimum set of simulations that need to be to carry out to assess the consequences properly. See Saravanan, Section 16.5.
Figure B2 shows the Keeling Curve observations of the global average level of Carbon Dioxide in Earth’s Atmosphere from 1958 to 2023, with the corresponding Temperature Curve easily calculated from Equation B1 using just as suggested in Aber (2022).
APPENDIX C
C1 Alternative Methods of Fitting to Multi-Wave Data
As already pointed in the Introduction the purpose of the paper is to the extend our published SL one-wave fitting method to multi-vave problems and to examine in particular its application to two important current problems.
Here we briefly mention two existing methods, each of which might possibly provide alternative approaches.
Spline functions are often used, particularly for interpolation purposes. The usual method of one dimensional spline fitting is to divide up the domain interval into separate section applying a separate spline function to each. Here problems can arise if the spline is a polynomial of high degree when one encounters the undesirable Runge’s (interpolation) phenomenon. where a small adjustment to make the interpolation better at one point leads to the butterfly effect of making distant points much worse.
In comparison we can regard our SL Multi-Wave Method as a spline method where each separate spline has the same infinite domain, with our parameterization characterizing decline in both directions, so that the parameters of each wave control only that wave.
An alternative is kriging which divides the fit into deterministic and stochastic components. However the method applies to processes that change randomly, not systematically linked. Also the method is technically complicated with, for example the regression coefficients defined in terms of the covariance matrix of the residuals. So only an expert would see how changes in the covariance matrix corresponds to wave behaviour.
In comparison each of the parameters, as defined in our version of the SL function, has an understandable geometrical meaning, even to a layperson, indicating the position, height, rate of increase and rate of decline of each wave.
REFERENCES (APPENDICES ONLY)
Aber J (2022) Quantitative Reasoning with Climate Data. Quantitative Reasoning with Climate Data - by John Aber (substack.com).
Maslin M (2021). Climate Change A Very Short Introduction. Oxford University Press, Oxford.
Saravanan R. (2022) The Climate Demon Past, Present, and Future of Climate Prediction. Cambridge University Press, Cambridge.