SMS: A Novel Approach for Bacterial Strain Analysis in Multiple Samples
Article Information
Saidi Wang1, Minerva Fatimae Ventolero2, Haiyan Hu1,3,# and Xiaoman Li2,#
1Department of Computer Science, University of Central Florida, Orlando, FL, 32816
2Burnett School of Biomedical Science, University of Central Florida, Orlando, FL, 32816
3Genomics and Bioinformatics Cluster, University of Central Florida, Orlando, FL, 32816
*Corresponding author: Haiyan Hu, Xiaoman Li, Burnett School of Biomedical Science, University of Central Florida, Orlando, FL, 32816, USA.
Received: 07 September 2023; Accepted: 13 September 2023; Published: 03 October 2023.
Citation:
Saidi Wang, Minerva Fatimae Ventolero, Haiyan Hu, Xiaoman Li. SMS: A Novel Approach for Bacterial Strain Analysis in Multiple Samples. Journal of Bioinformatics and Systems Biology. 6 (2023): 289-297.
View / Download Pdf Share at FacebookAbstract
The analysis of the bacterial strains is important for understanding drug resistance. Despite the existence of dozens of computational tools for bacterial strain studies, most of them are for known bacterial strains. Almost all remaining tools are designed to analyze individual samples or local strain regions. With multiple shotgun metagenomic samples routinely generated in a project, it is necessary to create methods to infer novel bacterial strain genomes in multiple samples. To fill this gap, we developed a novel computational approach called SMS to de novo reconstruct bacterial Strain genomes in Multiple Samples. Tested on 702 simulated and 195 experimental datasets, SMS reliably identified the strain number, abundance, and polymorphisms. Compared with two existing approaches, SMS showed superior performance.
Keywords
Bacterial strains, Shotgun metagenomics, Zero-inflated Poisson, Strain genome reconstruction
Bacterial strains articles; Shotgun metagenomics articles; Zero-inflated Poisson articles; Strain genome reconstruction articles
Bacterial strains articles Bacterial strains Research articles Bacterial strains review articles Bacterial strains PubMed articles Bacterial strains PubMed Central articles Bacterial strains 2023 articles Bacterial strains 2024 articles Bacterial strains Scopus articles Bacterial strains impact factor journals Bacterial strains Scopus journals Bacterial strains PubMed journals Bacterial strains medical journals Bacterial strains free journals Bacterial strains best journals Bacterial strains top journals Bacterial strains free medical journals Bacterial strains famous journals Bacterial strains Google Scholar indexed journals Shotgun metagenomics articles Shotgun metagenomics Research articles Shotgun metagenomics review articles Shotgun metagenomics PubMed articles Shotgun metagenomics PubMed Central articles Shotgun metagenomics 2023 articles Shotgun metagenomics 2024 articles Shotgun metagenomics Scopus articles Shotgun metagenomics impact factor journals Shotgun metagenomics Scopus journals Shotgun metagenomics PubMed journals Shotgun metagenomics medical journals Shotgun metagenomics free journals Shotgun metagenomics best journals Shotgun metagenomics top journals Shotgun metagenomics free medical journals Shotgun metagenomics famous journals Shotgun metagenomics Google Scholar indexed journals Zero-inflated Poisson articles Zero-inflated Poisson Research articles Zero-inflated Poisson review articles Zero-inflated Poisson PubMed articles Zero-inflated Poisson PubMed Central articles Zero-inflated Poisson 2023 articles Zero-inflated Poisson 2024 articles Zero-inflated Poisson Scopus articles Zero-inflated Poisson impact factor journals Zero-inflated Poisson Scopus journals Zero-inflated Poisson PubMed journals Zero-inflated Poisson medical journals Zero-inflated Poisson free journals Zero-inflated Poisson best journals Zero-inflated Poisson top journals Zero-inflated Poisson free medical journals Zero-inflated Poisson famous journals Zero-inflated Poisson Google Scholar indexed journals Strain genome reconstruction articles Strain genome reconstruction Research articles Strain genome reconstruction review articles Strain genome reconstruction PubMed articles Strain genome reconstruction PubMed Central articles Strain genome reconstruction 2023 articles Strain genome reconstruction 2024 articles Strain genome reconstruction Scopus articles Strain genome reconstruction impact factor journals Strain genome reconstruction Scopus journals Strain genome reconstruction PubMed journals Strain genome reconstruction medical journals Strain genome reconstruction free journals Strain genome reconstruction best journals Strain genome reconstruction top journals Strain genome reconstruction free medical journals Strain genome reconstruction famous journals Strain genome reconstruction Google Scholar indexed journals DNA articles DNA Research articles DNA review articles DNA PubMed articles DNA PubMed Central articles DNA 2023 articles DNA 2024 articles DNA Scopus articles DNA impact factor journals DNA Scopus journals DNA PubMed journals DNA medical journals DNA free journals DNA best journals DNA top journals DNA free medical journals DNA famous journals DNA Google Scholar indexed journals environments articles environments Research articles environments review articles environments PubMed articles environments PubMed Central articles environments 2023 articles environments 2024 articles environments Scopus articles environments impact factor journals environments Scopus journals environments PubMed journals environments medical journals environments free journals environments best journals environments top journals environments free medical journals environments famous journals environments Google Scholar indexed journals SMS articles SMS Research articles SMS review articles SMS PubMed articles SMS PubMed Central articles SMS 2023 articles SMS 2024 articles SMS Scopus articles SMS impact factor journals SMS Scopus journals SMS PubMed journals SMS medical journals SMS free journals SMS best journals SMS top journals SMS free medical journals SMS famous journals SMS Google Scholar indexed journals drug resistance articles drug resistance Research articles drug resistance review articles drug resistance PubMed articles drug resistance PubMed Central articles drug resistance 2023 articles drug resistance 2024 articles drug resistance Scopus articles drug resistance impact factor journals drug resistance Scopus journals drug resistance PubMed journals drug resistance medical journals drug resistance free journals drug resistance best journals drug resistance top journals drug resistance free medical journals drug resistance famous journals drug resistance Google Scholar indexed journals metagenomic articles metagenomic Research articles metagenomic review articles metagenomic PubMed articles metagenomic PubMed Central articles metagenomic 2023 articles metagenomic 2024 articles metagenomic Scopus articles metagenomic impact factor journals metagenomic Scopus journals metagenomic PubMed journals metagenomic medical journals metagenomic free journals metagenomic best journals metagenomic top journals metagenomic free medical journals metagenomic famous journals metagenomic Google Scholar indexed journals
Article Details
1. Introduction
Bacteria are ubiquitous and play crucial roles in disease progression and human health [1-8]. Multiple strains of a bacterial species usually coexist in an environmental niche. These strain genomes of the same species are different from each other, with small variations such as single nucleotide polymorphisms (SNPs), different gene contents, and/or different plasmid genes [9]. Such a difference results in different fitness to survive or react to stimuli, which is often the cause of different host responses, drug resistance, mixed infection, etc. [10, 11]. It is thus important to study and reconstruct bacterial strain genomes. Shotgun metagenomic sequencing is routinely employed to study microbes and reconstruct bacterial genomes [1, 6, 8, 12-14]. In shotgun metagenomics, the DNA of all species and strains in a clinical or environmental sample is randomly fragmented and sequenced. These sequenced DNA fragments called reads are then applied to infer the present species, their abundance, functionality, etc. Because reads are short and mixed from different species, it is still challenging to study low-abudnant species and strains in shotgun metagenomics [15-18]. Moreover, current assembly methods usually cannot distinguish different strains of the same species, which leaves most studies on taxons no lower than the species level and the strain analysis still at its infancy [18, 19]. On the other hand, with the sequencing cost dramatically decreasing, multiple shotgun metagenomic samples are often available from the same type of environments or clinical setups [20-22]. The multiple samples from the same or similar environmental niche are likely to share bacterial strains and thus provide an unprecedented opportunity to study and reconstruct bacterial strain genomes [20-22]. Dozens of computational methods are available to infer bacterial strains from shotgun metagenomic reads [16, 23-37]. Most of them rely on prior knowledge of known strains, and they have successfully identified known strains while cannot be applied to study new strains that commonly exist. A handful of methods that do not depend on known strains are thus developed, which can be divided into two groups [27, 29, 31-33, 38, 39]. One group defines strain variations and strains based on species-specific marker genes, which can significantly speed up the process of analyzing a large number of species in a microbiome while depending on the quality and quantity of the marker genes [32, 38]. The other group considers the SNPs across the entire reference genomes of a species instead of only the marker gene regions, which can delineate the strain genomes in detail and are important for studying individual pathogen species [16, 26, 28, 29]. These methods have shed new light on bacterial strains in environmental samples. However, their performance is still suboptimal in terms of the predicted strain number and abundance. For instance, a recent method, StrainFinder, did not have good accuracy in predicting strain SNPs and strain abundance, even provided with the correct strain number [26, 40]. To accurately identify strains in shotgun metagenomic samples, we developed a novel method called SMS (Strains in Multiple Samples). Starting from a species genome, SMS de novo reconstructs its strain genomes from shtogun reads in multiple shotgun metagenomic samples. It models the coverage of every strain in individual samples by zero-inflated Poisson (ZIP) distributions and classifies SNPs with adaptively inferred centers, which enables it to identify low-coverage strains and predict strains with high accuracy. Tested on 702 simulated and 195 experimental datasets, SMS accurately predicted the strain number, abundance, and SNPs. Compared with two recent approaches, SMS showed much better performance.
2. Materials and Methods
SMS reconstructs bacterial strain genomes with a reference genome and raw reads in multiple shotgun metagenomic samples (Fig. 1). The basic assumption is that different SNPs from the same strain follow a common ZIP distribution in a sample, and SNPs from different strains follow different ZIP distributions in individual samples. Assume there are R strains of a species of interest in m samples. Starting from the cleaned raw reads, SMS defines SNPs based on the reads mapped to the reference. Because of the species reference genome, SMS considers only the mixed reads in shotgun metagenomic samples that are mapped to the reference genome. In other words, SMS considers only the reads from one species in the m samples, as most reads mapped to the reference genome are likely from the reference species. Considering only one species makes sense because we often have a pathogen of interest and want to study its strains in clinical or environmental samples in practice. With the mapped reads, SMS then determines the initial strains and their abundance with the pooled sample, the combined m samples. Next, SMS refines the initial strains and their abundance based on the SNP coverage patterns across samples. The rationale is that SNPs from the same strain will have more similar coverage patterns across samples than SNPs from different strains. Finally, SMS outputs the predicted strains and their abundance. The details are in the following sections.
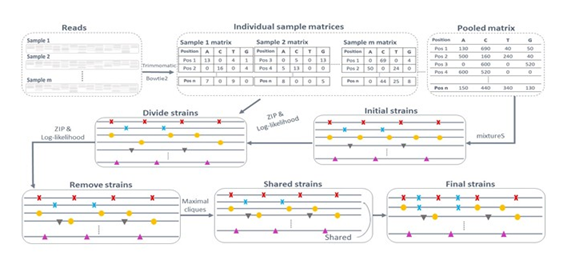
Figure 1: The SMS workflow.
2.1 Identification of potential SNPs
With reads from the m samples, SMS trims reads, and filters low-quality reads with the tool trimmomatic [41]. SMS then maps the cleaned reads to the reference genome by bowtie2 [42]. In every sample, SMS obtains a 4 by n sample-specific matrix composed of the frequencies of A, C, G, and T in the mapped reads at each of the n reference genome positions. Similarly, SMS acquires a pooled matrix of 4 by n for the pooled sample, the sum of the m sample-specific matrices. SMS then determines the n' potential polymorphic positions based on these m+1 matrices. A reference genome position is potentially polymorphic if the following criteria are satisfied: 1). It has a coverage larger than 10% of the pooled coverage. The coverage of a genome (position or SNP) is calculated as the average number of reads mapped to this genome (position or SNP); 2). It has at least two nucleotides, each with no smaller than 5% of the pooled coverage. Note that when the reference nucleotide at a position has fewer than 5% of the pooled coverage, the reference nucleotide is replaced with the most frequent nucleotide at this position; 3). Each of its two most frequent nucleotides must occur in at least 5% of the m samples. Finally, SMS considers all n1 nucleotides with coverage larger than 5% of the genome coverage at these positions as potential SNPs, where n'≤n1≤3n'. Note that despite the default requirement of at least 5% of the pooled coverage for any strain to be identified, SMS can identify low-abundance strains in multiple samples. A low-abundance strain may account for fewer than 0.01% of a metagenome. However, with a few dozen samples, its species may already have a reasonable coverage in the pooled sample, and SMS will identify each of its strains with at least 5% of the pooled species coverage in the pooled sample. As demonstrated in the following simulated studies, with the pooled species coverage 100X, SMS identified strains with a pooled coverage of 10X in 214 out of 216 datasets for three randomly chosen bacterial species.
2.2 Prediction of the strain number and abundance
With the n1 potential SNPs, SMS infers the strain number and abundance in four steps.
First, SMS obtains an initial number of strains and their SNPs. SMS applies mixtureS to the above n1 SNPs with the pooled sample and outputs the predicted strains and their abundance. MixtureS reconstructs the strain genomes instead of local strain regions corresponding to marker genes from shotgun reads in one sample and has shown good performance previously [26, 40]. In this way, the strains with different pooled coverage are separated into R strains. R is automatically inferred.
Second, SMS refines the predicted strains so that almost all SNPs in an actual strain are assigned to one predicted strain. Since the coverage of SNPs from the same strain is expected to follow the same ZIP distributions in individual samples, the coverage vectors of two SNPs from the same strain are more similar than those of two SNPs from different strains. Here the coverage vector of an SNP is a vector composed of its coverage in the m samples. The similarity measurement of two vectors is described in the next section. Based on this observation, SMS iteratively regroups the n1 SNPs into R groups so that SNPs from the same group have more similar vectors. Starting from the predicted R strains by mixtureS, the majority of SNPs in each of which are likely from the same strain, SMS represents each strain by an m by 1 coverage vector, the average of the coverage vectors of the SNPs currently assigned to this strain. SMS then reassigns each of the n1 SNPs to the strain with the most similar coverage vector to the coverage vector of this SNP. With the reassigned SNPs, the coverage vectors of the strains are recalculated. This process is repeated a given number of times or until the assigned SNPs to each strain do not change. In this way, the coverage vector of each predicted strain and the assignment of the n1 SNPs become more and more accurate, with almost all SNPs from an actual strain grouped together.
Third, SMS investigates whether there are more or fewer than R strains. SMS divides each strain into two strains, one strain at a time. To determine whether a strain should be divided, SMS models each strain in a sample by a ZIP distribution, estimates the parameters of the ZIP distributions, and calculates the likelihood ratio of observing the SNPs in this strain across the m samples to that in two divided strains. The details of the ZIP parameter estimation and the likelihood testing are in the following sections. A strain is divided only when its division significantly increases the likelihood (Chi-square test p-value<0.001). If a strain is divided, SMS considers whether the two new divided strains can be further divided similarly. This process is repeated until no strain can be further divided. With all possible divisions that significantly increase the likelihood, SMS obtains the updated R strains and repeats Step two to reassign the n1 SNPs to these R strains again. SMS then considers removing each strain, one strain at a time. The process is similar to dividing a strain based on the ZIP parameter estimation and the likelihood test.
Finally, SMS removes the predicted strains that are majorly composed of shared SNPs by multiple strains and reassigns their SNPs to the corresponding strains. To remove a strain, SMS identifies its consistent strains. Strain one is a consistent strain of strain two if every entry in the coverage vector of strain one is no large than the corresponding entry in the coverage vector of strain two plus a small cutoff. Similarly, multiple strains together are consistent with strain two if the sum of the corresponding entries in their coverage vectors is no large than the corresponding entry in the coverage vector of strain two plus the same cutoff. With the consistent strains of a strain, SMS constructs a graph, with each consistent strain as a node and edges connecting pairs of strains that are together still consistent with this strain. SMS then identifies the largest cliques in this graph with the corresponding groups of strains together consistent with this strain. With a clique identified, SMS removes this strain and reassigns its SNPs to all consistent strains in this clique. In this way, SMS finalizes the predicted strains and their SNPs. The abundance of every strain is calculated as the average coverage of the SNPs unique to this strain.
2.3 The similarity of two coverage vectors
SMS calculates the similarity of two coverage vectors (a_1,a_2,…,a_m) and (b_1,b_2,…,b_m) by a pre-defined regression formula: 79.25d+ 43.06(c+c3)-0.04/(0.0025+d), where d is the distance between the two vectors, and c is their Kendall rank correlation. This formula was constructed based on a set of 18 pre-simulated training datasets. SMS chooses this similarity measurement, because it shows better performance than others, including correlation, Euclendian distance, relative entropy, etc.
2.4 ZIP model of a strain in a sample
SMS models the coverage of the SNPs from the p-th strain in the q-th sample by a ZIP distribution ZIP(x, πpq, λpq ) when the p-th strain occurs in the q-th sample, where 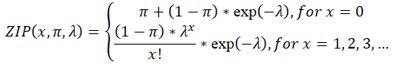
Assume we have an n1 by m matrix, X=(x_ij ), which store the coverage of the above n1 SNPs in the m samples. Assume Z=(z_ir ) is the indicator to tell whether the i-th SNP belongs to the r-th strain, where 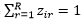 for all i from 1 to n1 and zir can be only 0 or 1. Assume Y=(y_jr ) is the indicator to show whether the r-th strain occurs in the j-th sample, where y_jr can be only 0 or 1. If at least one SNP from a strain has a non-zero coverage in a sample, we tentatively claim that this strain occurs in this sample. When yjr=1, we also define ,
for all i from 1 to n1 and zir can be only 0 or 1. Assume Y=(y_jr ) is the indicator to show whether the r-th strain occurs in the j-th sample, where y_jr can be only 0 or 1. If at least one SNP from a strain has a non-zero coverage in a sample, we tentatively claim that this strain occurs in this sample. When yjr=1, we also define , 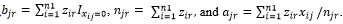
To estimate the parameters in the ZIP, for a given strain that occurs in a given sample, say the r-th strain in the j-th sample (i.e., yjr=1), SMS initializes 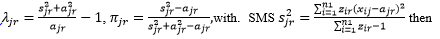 uses the following iteration method to obtain the maximal likelihood estimation of π_jr and λ_jr: first replaces πjr by
uses the following iteration method to obtain the maximal likelihood estimation of π_jr and λ_jr: first replaces πjr by 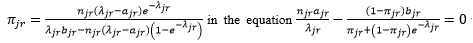 to obtain an equation of λjr, then solves this equation by the Newton’s iteration method. Everywhere in this process, if πjr=0, you will directly estimate λjr= ajr.
to obtain an equation of λjr, then solves this equation by the Newton’s iteration method. Everywhere in this process, if πjr=0, you will directly estimate λjr= ajr.
2.5 Log likelihood test
Given R strains, the full likelihood of observation the frequencies of these n1 SNPs in the m samples is
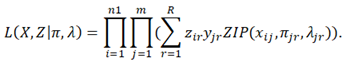
When SMS splits one strain into two or removes one strain, the likelihood can be similarly calculated. To assess the significance of changing the current R strains, we calculate the ratio of the likelihood after changing (split or remove) to the likelihood before changing. The ratio approximately follows a Chi-square distribution with the degree of freedom equal to the difference of the parameters in the two models. If the Chi-square test p-value is smaller than a pre-defined cutoff, SMS correspondingly modifies the current R strains.
2.6 Simulated and experimental datasets
We simulated 702 datasets (Supplementary Table S1). As mentioned above, because SMS uses a species reference genome, we only need to consider reads from one species in a dataset. We thus simulated data with only one species in each dataset. In every dataset, a species reference genome was randomly chosen, 2 to 4 strains were simulated, and 5 to 35 samples were generated. For each reference genome, their four strains were generated by randomly choosing 0.01% of the genome positions and then randomly substituting the reference nucleotide with another nucleotide. This 0.01% mutation rate was from previous studies [16, 28], representing relatively more similar strains of a species (99.99% sequence identities) that are thus more challenging to distinguish from each other. The read coverage of a reference genome in a dataset was one of the following four coverage, 100x, 150x, 200x, and 300x. The number of strains and their relative abundance in a dataset were specified by one of the following five configurations: 10:20:30:40, 10:25:25:40, 10:30:60, 15:30:55, and 30:70. For a dataset, with the chosen configuration and the number of samples, a subset of samples were randomly chosen for each strain and the coverage of this strain in one of the samples was then randomly determined so that the pooled coverage of this strain was the same as what was specified in the configuration. With the coverage of strains in a sample, paired reads of 100 base pairs long were randomly generated using dwgsim. We tested SMS on 195 experimental datasets [11]. Each dataset is known to have two Mycobacterium tuberculosis strains with predicted abundance. The abundance is inferred from two different computational methods. The actual SNPs in each strain are unknown.
2.7 Comparison with existing methods
We compared SMS with mixtureS and StrainFinder in a desktop computer with the Intel Core i9-9900KF CPU (16 cores@3.6GHz) and 32 gigabytes memory. We used the following commands to run the three tools respectively:
SMS: python SMS/running.py --output_name %s --genome_len %s --genome_name %s --genome_file_loc %s --bam_loc_file %s --res_dir %s
MixtureS: python mixtureS/mixture_model.py --sample_name %s --genome_len %s --genome_name %s --genome_file_loc %s --bam_file %s --res_dir %s
StrainFinder: python StrainFinder/StrainFinder.py --aln %s -N %s --max_reps 10 --dtol 1 --ntol 2 --max_time 3600 --coverage --em_out %s --out_out %s --log %s --n_keep %s --force_update --merge_out –msg
3. Results
3.1 SMS correctly predicted the strain numbers
We studied the number of strains predicted in 702 simulated datasets (Supplementary Table S1). There were 5 to 35 samples and 2 to 4 strains in every dataset, with the pooled coverage of strains from 100X to 300X. The pooled coverage was the sum of the coverage of all strains of a species in all samples. The number of strains and their relative abundance are specified by one of the following five configurations in each dataset: 10:20:30:40, 10:25:25:40; 10:30:60, 15:30:55, and 30:70. For instance, for a dataset with the configuration 10:20:30:40, the proportion of reads from the four strains was 10%, 20%, 30% and 40%, respectively.
Overall, SMS predicted the correct strain numbers in all but five datasets (Supplementary Tables S2-S5). Interestingly, SMS did not predict the correct strain number in at least one dataset for each of the three randomly selected species, implying that its performance was not species-specific. In each of the five datasets, a pair of strains shared 30% of their SNPs. In four of the five datasets, three strains shared 20% of their SNPs. These shared SNPs may have confused SMS when the coverage was 100X. When the coverage was increased, SMS predicted the correct strain number in each of the five corresponding datasets. These analyses suggested that SMS can accurately predict the strain number, even when the pooled coverage was 100X, and there were only five samples in a dataset. Moreover, the predicted strain number was even more accurate with a larger pooled coverage (200X coverage for perfect prediction here).
3.2 SMS reliably estimated the strain abundance
We investigated how well SMS predicted the strain abundance. No matter whether the strain number was correctly predicted, the predicted strain abundance agreed well with the known strain abundance (Fig. 2, Supplementary Tables S2-S5). This agreement did not depend on the sample number, the pooled coverage, the strain number, etc.

Figure 2: The predicted strain abundance. A) Unshared datasets; B) Shared datasets; and C) All datasets.
MAE is the average Maximal Absolute Difference between the predicted abundance and the corresponding true abundance across datasets.
In the 697 datasets SMS correctly predicted the strain number, the predicted strain abundance was within 97.31% of the true abundance. The mean and median ratio of the predicted abundance to the true abundance were 0.99 and 1.00, respectively. Even in the five datasets with the incorrectly predicted strain number, the predicted strain abundance was similar to the true abundance. For instance, SMS predicted four strains in three datasets with three strains (Supplementary Table S5). In two datasets, two strains had a predicted abundance of about 0.08 and 0.29, respectively, which were close to the corresponding true abundance of 0.10 and 0.30. The two remaining predicted abundance were about 0.42 and 0.21, which differed from the third true abundance, 0.60. In the third dataset, one strain was predicted with an abundance of 0.31, close to the true abundance of 0.30. The wrong prediction of the strain number and strain abundance was likely due to the third strain’s uneven and relatively limited coverage. After increasing the coverage, SMS predicted the correct strain number and more similar abundance (Supplementary Table S5).
The accuracy was in general improved with more samples and a larger pooled coverage in a dataset (Fig. 2). For instance, when the sample number was larger, the median of the predicted abundance was closer to the true abundance, and the variation of the maximal absolute difference (MAE) between the predicted abundance and the true abundance was smaller. The accuracy was not affected much by different species or the number of strains in a dataset (Fig. 2). For instance, the MAE was within a similar range and with a similar mean/median when there were different numbers of strains. The small variations suggested that the predicted abundance by SMS was robust to different bacterial genomes, different numbers of strains, etc.
3.3 SMS faithfully determined the SNPs
Existing methods mainly focus on the predicted strain number and only occasionally consider their abundance. Rarely do they mention the accuracy of the predicted strain SNPs. With the simulated datasets, we systematically evaluated the predicted SNPs. We found that SMS has a precision of 0.97 and a recall of 0.96 to predict strain SNPs.
We studied the datasets without shared SNPs among strains (Supplementary Table S6). In all 216 datasets, on average, SMS had a precision of 0.98 and a recall of 0.98. For a given species with a specified pooled coverage, the precision and recall were higher on datasets with more samples in general. Similarly, they were generally higher on datasets with a larger pooled coverage when the species and the sample number were fixed. For instance, for the reference species genome NC_009515.1 and the sample number 20, the precison increased from 0.98 to 0.99 and the recall increased from 0.97 to 0.99 when the pooled coverage increased from 100X to 300X.
We also studied the predicted strains on datasets with shared SNPs among strains (Supplementary Tables S7-S9). We again focused on the two most challenging configurations: 10:20:30:40 and 10:25:25:40. They were challenging because the shared SNPs among strains may have similar coverage across samples with SNPs unique to other strains. For instance, the shared SNPs between the first two strains in the configuration 10:20:30:40 had a relative abundance of 30%, the same as the relative abundance of the third strain. Even with such complexity, SMS on average had a precision of 0.97 and a recall of 0.96 on all datasets (Supplementary Tables S7 and S8). The performance suggested that SMS could reconstruct the complicated evolutionary trajectories of strains with shotgun sequencing reads.
3.4 SMS performed well on experimental datasets
We tested SMS on 195 experimental datasets (Supplementary Table S10). We chose these datasets because their strain numbers were known. The strain abundance was also predicted previously [11]. Note that the datasets from the Critical Assessment of Metagenome Interpretation challenge did not provide the strain number, strain abundance and SNPs unique to strains, thus not suitable for the strain genome reconstruction here [18].
SMS identified two strains in each of these 195 datasets, which agreed well with the previous study [11]. This study showed that there were at least 11 heterozygous sites in each of these 195 datasets. Interestingly, SMS showed that the two strains in different datasets were the same, which was consistent with the fact that these datasets were from clinical samples collected from the same region. Moreover, SMS distinguished strains with similar abundance in these datasets. For instance, in the dataset ERR323056, there were 69 heterozygous sites observed in reads [11]. SMS predicted two strains with a relative abundance of 0.52 and 0.48. The previous study based on the SNP frequency identified only one strain, likely due to their similar abundance. Since the strain abundance was unknown, we compared the predicted abundance by SMS and the previous study. The difference between the predicted strain abundance to the predicted abundance previously had a mean and median of 0.16 and 0.12, respectively, if we considered only the 186 datasets where the previous study correctly predicted the strain number.
3.5 SMS reconstructed strain genomes better than existing methods
We compared SMS with mixtureS [26] and StrainFinder [29]. We did not compare other tools because mixtureS and StrainFinder showed better performance previously, and other tools may only work for marker gene regions instead of on the genome-scale [26]. Since mixtureS works on one sample, we ran it on the pooled sample in each dataset. Because StrainFinder cannot determine the strain numbers, we specified the known strain numbers in the corresponding datasets.
We compared the strain number, abundance and SNPs predicted by the three methods. SMS performed much better than others (Table 1). For instance, for simulated datasets with no shared SNPs among strains, SMS predicted the correct strain number in all 216 datasets while mixtureS correctly predicted the strain number in 98 datasets. On average, the predicted SNPs by SMS had a precision of 0.97 and a recall of 0.98, larger than those of mixtureS and SStrainFinder. Moreover, the predicted strain abundance by SMS had an average MAE of 0.004, compared with 0.08 by mixtureS and 0.07 by StrainFinder.
Table 1: The performance of the three tools
|
Dataset |
SMS |
mixtureS |
StrainFinder |
||||||
|
# (%) of datasets |
Precision, Recall, F1 |
MAE |
# (%) of datasets |
Precision, Recall, F1 |
MAE |
Precision, Recall, F1 |
MAE |
||
|
702 simulated datasets |
Unshared |
216 (100%) |
0.97, 0.98, 0.98 |
0.004 |
98 |
0.81, 0.83, 0.80 |
0.08 |
0.66, 0.56, 0.53 |
0.07 |
|
-45.37% |
|||||||||
|
Shared |
481 |
0.97, 0.96, 0.96 |
0.008 |
184 |
0.83, 0.58, 0.63 |
0.07 |
0.68, 0.56, 0.56 |
0.06 |
|
|
-98.97% |
37.86% |
||||||||
|
All |
697 (99.29%) |
0.97, 0.96,0.96 |
0.007 |
282 |
0.82, 0.66, 0.68 |
0.07 |
0.68, 0.56, 0.55 |
0.06 |
|
|
40.17% |
|||||||||
|
195 experimental datasets |
195 |
NA |
0.16 |
146 |
NA |
0.12 |
NA |
0.26 |
|
|
-100% |
74.87% |
||||||||
The three columns for each tool are the number (percentage) of datasets where the tool predicted the correct strain number; the precision, recall and F1 score of the predicted strain SNPs; and the average MAE of the predicted strain abundance.
We also studied the running time of different methods (Supplementary Table S11). SMS took a little more time to run than mixtureS. However, the difference was not so evident. For all tools, the time cost mainly depended on the number of strains and SNPs, instead of the dataset sizes.
4. Discussion
SMS reconstructs bacterial strain genomes with multiple shotgun metagenomic samples. It considers the coverage variation of individual strains across samples to distinguish strains of the same bacterial species. As demonstrated in simulated and experimental datasets, SMS is able to separate strains with similar abundance. The capability to separate strains with similar abundance is in general improved with more samples and larger pooled coverage.
SMS reconstructs bacterial strain genomes with a species reference genome and the raw sequencing reads. The reference is employed to map the cleaned reads. The chosen reference thus does not affect the predicted strain number and abundance, as they are inferred from the SNPs in strains that come from the mapped reads. SMS defines SNPs with an in-house procedure, which may affect the quality of individual SNPs. However, we do not think that the potential false SNPs will affect the predicted strain number and abundance, as they are determined by the coverage of the majority of SNPs in individual strains. Users may choose existing tools like SAMtools [43] to define SNPs in samples. Moreover, since reads are mapped to the reference genomes in advance, SMS can be applied to general metagenomic datasets instead of the simulated shotgun samples for individual species illustrated here.
SMS is not designed for the strain analysis of novel species. With more and more sequenced bacterial genomes, this issue may not be of concern in the future. Moreover, SMS considers only the reference genomic regions to reconstruct bacterial strain genomes. It thus does not consider accessory genes that are not represented in the chosen reference genomes. In this sense, what SMS reconstructs is similar to the strain core genomes but may include additional reference-specific regions. In the future, one may apply other machine learning and data mining methods [44-48] to further discover accessory genes in strains, with the inferred strain number and abundance in samples.
Author Contributions
H.H. and X.L. designed the study. S.W., M.V., H.H. and X.L. analyzed data and wrote the manuscript.
Acknowledgments
This work was supported by the National Science Foundation [1661414, 2015838, 2120907].
Conflict of interest
The authors declare no cometing interests.
References
- Methe BA, Nelson KE, Pop M, et al. A framework for human microbiome research, Nat 486 (2012): 215-221.
- Proctor LM, Creasy HH, Fettweis HM, e al. The Integrative Human Microbiome Project. Nat 569 (2019): 641-648.
- Proctor LM, et al. The Integrative Human Microbiome Project: Dynamic Analysis of Microbiome-Host Omics Profiles during Periods of Human Health and Disease. Cell host & microbe 16 (2014): 276-289.
- Rasko H, Sperandio V. Anti-virulence strategies to combat bacteria-mediated disease. Nat Rev Drug Discov 9 (2010): 117-128.
- Tyson GW, Chapman J, Hugenholtz P, et al. Community structure and metabolism through reconstruction of microbial genomes from the environment. Nat 428 (2004): 37-43.
- Venter JC, Remington K, Heidelberg JF, et al. Environmental genome shotgun sequencing of the Sargasso Sea. Sci 304 (2004): 66-74.
- Wang Y, Goodison S, Li X, et al. Prognostic cancer gene signatures share common regulatory motifs. Sci Rep 7 (2017): 4750.
- Wooley JC, Godzik A, Friedberg I. A primer on metagenomics, PLoS comp biol 6 (2010): 1000667.
- Van Rossum T, Ferretti P, Maistrenko OM, et al. Diversity within species: interpreting strains in microbiomes. Nat Rev Microbiol 18 (2020): 491-506.
- Eyre DW, Cule ML, Griffiths D, et al. Detection of mixed infection from bacterial whole genome sequence data allows assessment of its role in Clostridium difficile transmission. PLoS Comp Boil 9 (2013): 1003059.
- Sobkowiak B, Glynn JR, Mallard K, et al. Identifying mixed Mycobacterium tuberculosis infections from whole genome sequence data. BMC genomics 19 (2018): 613.
- Eisen JA. Environmental shotgun sequencing: its potential and challenges for studying the hidden world of microbes, PLoS Boil 5 (2007): 82.
- Li X, Naser SA, Khaled A, et al. When old metagenomic data meet newly sequenced genomes, a case study. PloS One 13 (2018): 0198773.
- Wang Y, Hu H, Li X. MBMC: An Effective Markov Chain Approach for Binning Metagenomic Reads from Environmental Shotgun Sequencing Projects, Omics: J Int Biol 20 (2016): 470-479.
- Cleary B, Brito IL, Huang K, et al. Detection of low-abundance bacterial strains in metagenomic datasets by eigengenome partitioning, Nat Biotech 33 (2015): 1053-1060.
- Li X, Saadat S, Hu HY, et al. BHap: a novel approach for bacterial haplotype reconstruction. Bioinfo 35 (2019): 4624-4631.
- Kyrgyzov O, Prost V, Gazut S, et al. Bruls, Binning unassembled short reads based on k-mer abundance covariance using sparse coding, Giga Sci 9 (2020).
- Sczyrba A, Hofmann P, Belmann P, et al. Critical Assessment of Metagenome Interpretation-a benchmark of metagenomics software. Nat Methods 14 (2017): 1063-1071.
- Van der Walt AJ, Van Goethem MW, Ramond JB, et al. Assembling metagenomes, one community at a time. BMC Genomics 18 (2017).
- Gevers D, Kugathasan S, Knights D, et al. A Microbiome Foundation for the Study of Crohn's Disease. Cell host & Microbe 21 (2017): 301-304.
- Parks DH, Rinke C, Chuvochina M, et al. Recovery of nearly 8,000 metagenome-assembled genomes substantially expands the tree of life. Nat Microbiol 2 (2017): 1533-1542.
- Pasolli E, Asnicar F, Manara S, et al. Extensive Unexplored Human Microbiome Diversity Revealed by Over 150,000 Genomes from Metagenomes Spanning Age, Geography, and Lifestyle. Cell 176 (2019): 649-670.
- Albanese D, Donati C. Strain profiling and epidemiology of bacterial species from metagenomic sequencing. Nat Commun 8 (2017).
- Anyansi C, Straub TJ, Manson AL, et al. Computational Methods for Strain-Level Microbial Detection in Colony and Metagenome Sequencing Data. Front Microbiol 11 (2020): 1925.
- Hong CJ, Manimaran S, Shen Y, et al. PathoScope 2.0: a complete computational framework for strain identification in environmental or clinical sequencing samples. Microbiome 2 (2014).
- Li X, Hu H, Li X. MixtureS: a novel tool for bacterial strain reconstruction from reads. Bioinfo (2020).
- Luo C, Knight R, Siljander H, et al. ConStrains identifies microbial strains in metagenomic datasets, Nat Biotechnol 33 (2015): 1045-1052.
- Pulido-Tamayo S, Sanchez-Rodriguez A, Swings T, et al. Frequency-based haplotype reconstruction from deep sequencing data of bacterial populations, Nucleic Acid Res 43 (2015): 105.
- Smillie CS, Sauk J, Gevers D, et al. Strain Tracking Reveals the Determinants of Bacterial Engraftment in the Human Gut Following Fecal Microbiota Transplantation. Cell host & Microbe 23 (2018): 229-350.
- Ahn TH, Chai JJ, Pan CL. Sigma: Strain-level inference of genomes from metagenomic analysis for biosurveillance, Bioinfo 31 (2015): 170-177.
- Costea PI, Munch R, Coelho LP, et al. metaSNV: A tool for metagenomic strain level analysis. PloS One 12 (2017): 0182392.
- Nayfach S, Rodriguez-Mueller B, Garud N, et al. An integrated metagenomics pipeline for strain profiling reveals novel patterns of bacterial transmission and biogeography. Genome Res 26 (2016): 1612-1625.
- Quince C, Delmont TO, Raguideau SJ, et al. DESMAN: a new tool for de novo extraction of strains from metagenomes. Genome Biol 18 (2017): 181.
- Roosaare M, Vaher M, Kaplinski L, et al. StrainSeeker: fast identification of bacterial strains from raw sequencing reads using user-provided guide trees. PeerJ 5 (2017): 3353.
- Sankar A, Malone B, Bayliss SC, et al. Bayesian identification of bacterial strains from sequencing data. Microb Genome 2 (2016): 000075.
- Scholz M, Ward DV, Pasolli E, et al. Strain-level microbial epidemiology and population genomics from shotgun metagenomics, Nat Methods 13 (2016): 435-438.
- Tamburini FB, Andermann TM, Tkachenko E, et al. Precision identification of diverse bloodstream pathogens in the gut microbiome. Nat Med 24 (2018): 1809-1814.
- Truong DT, Tett A, Pasolli E, et al. Microbial strain-level population structure and genetic diversity from metagenomes. Genome Res 27 (2017): 626-638.
- Quince C, Nurk S, Raguideau S, et al. STRONG: metagenomics strain resolution on assembly graphs. Genome Biol 22 (2021): 214.
- Ventolero MF, Wang S, Hu H, et al. Computational analyses of bacterial strains from shotgun reads. Briefings in Bioinfo 23 (2022).
- Bolger AM, Lohse M, Usadel B. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinfo 30 (2014): 2114-2120.
- Langmead B, Salzberg SL. Fast gapped-read alignment with Bowtie 2. Nat Methods 9 (2012): 357-359.
- Li H, Handsaker B, Wysoker A, et al. Genome Project Data Processing, The Sequence Alignment/Map format and SAMtools, Bioinfo 25 (2009): 2078-2079.
- Murphy K. Machine Learning: A Probabilistic Perspective. The MIT Press (2012).
- Talukder A, Saadat S, Li X, et al. EPIP: a novel approach for condition-specific enhancer-promoter interaction prediction. Bioinfo 35 (2019): 3877-3883.
- Tibshirani R, Wang P. Spatial smoothing and hot spot detection for CGH data using the fused lasso. Biostatistics 9 (2008): 18-29.
- Zhao C, Li X, Hu H. PETModule: a motif module based approach for enhancer target gene prediction. Sci Rep 6 (2016): 30043.
- Zhou J, Liu J, Narayan VA, et al. Modeling Disease Progression via Fused Sparse Group Lasso. KDD 2012 (2012): 1095-1103.
