Identification of Methods for Estimating Knee Rotation Axis
Article Information
Maude Traullé1,2, Jean Mazeas1, Amaury Vandebrouck3, Pascal Duffiet3, Louis Ratte3, Florian Forelli1,2 ?
1Researcher Physical Therapist in OrthoLab, Clinic of Domont, 85 route de Domont 95330 Domont, France
2Co-Director in OrthoLab, OrthoLab, Clinic of Domont, 85 route de Domont 95330 Domont, France
3Orthopaedic Surgeon, Clinic of Domont, 85 route de Domont 95330 Domont, France
*Corresponding Author: Dr. Florian Forelli, OrthoLab, Clinic of Domont, 85 route de Domont 95330 Domont, France
Received: 7 April 2020; Accepted: 15 April 2020; Published: 21 April 2020
Citation: Maude Traullé, Jean Mazeas, Amaury Vandebrouck, Pascal Duffiet, Louis Ratte, Florian Forelli. Identification of Methods for Estimating Knee Rotation Axis. Journal of Orthopaedics and Sports Medicine 2 (2020): 108-115.
View / Download Pdf Share at FacebookAbstract
The Quantified Motion Analysis (QMA) has become in recent years a clinical examination whose understanding and improvement are being developed. Based on a three-dimensional projection of the body segments, the QMA must define these segments and their means of union, the axes and centers of articular rotation. Two main techniques exist: predictive estimation techniques and functional techniques which use a calibration movement to estimate the axes and centers of rotation. These latter techniques, known as functional, seem to show superiority in terms of reproducibility of the estimate of the axis of rotation of the knee, but no consensus exists. The same applies to the calibration movements used.
Keywords
Gait analysis; Plug in Gait; Axe of rotation; Calibration movement
Human movement articles Human movement Research articles Human movement review articles Human movement PubMed articles Human movement PubMed Central articles Human movement 2023 articles Human movement 2024 articles Human movement Scopus articles Human movement impact factor journals Human movement Scopus journals Human movement PubMed journals Human movement medical journals Human movement free journals Human movement best journals Human movement top journals Human movement free medical journals Human movement famous journals Human movement Google Scholar indexed journals Soft tissue articles Soft tissue Research articles Soft tissue review articles Soft tissue PubMed articles Soft tissue PubMed Central articles Soft tissue 2023 articles Soft tissue 2024 articles Soft tissue Scopus articles Soft tissue impact factor journals Soft tissue Scopus journals Soft tissue PubMed journals Soft tissue medical journals Soft tissue free journals Soft tissue best journals Soft tissue top journals Soft tissue free medical journals Soft tissue famous journals Soft tissue Google Scholar indexed journals Bone articles Bone Research articles Bone review articles Bone PubMed articles Bone PubMed Central articles Bone 2023 articles Bone 2024 articles Bone Scopus articles Bone impact factor journals Bone Scopus journals Bone PubMed journals Bone medical journals Bone free journals Bone best journals Bone top journals Bone free medical journals Bone famous journals Bone Google Scholar indexed journals Skeletal movement articles Skeletal movement Research articles Skeletal movement review articles Skeletal movement PubMed articles Skeletal movement PubMed Central articles Skeletal movement 2023 articles Skeletal movement 2024 articles Skeletal movement Scopus articles Skeletal movement impact factor journals Skeletal movement Scopus journals Skeletal movement PubMed journals Skeletal movement medical journals Skeletal movement free journals Skeletal movement best journals Skeletal movement top journals Skeletal movement free medical journals Skeletal movement famous journals Skeletal movement Google Scholar indexed journals Hip articles Hip Research articles Hip review articles Hip PubMed articles Hip PubMed Central articles Hip 2023 articles Hip 2024 articles Hip Scopus articles Hip impact factor journals Hip Scopus journals Hip PubMed journals Hip medical journals Hip free journals Hip best journals Hip top journals Hip free medical journals Hip famous journals Hip Google Scholar indexed journals Ankle articles Ankle Research articles Ankle review articles Ankle PubMed articles Ankle PubMed Central articles Ankle 2023 articles Ankle 2024 articles Ankle Scopus articles Ankle impact factor journals Ankle Scopus journals Ankle PubMed journals Ankle medical journals Ankle free journals Ankle best journals Ankle top journals Ankle free medical journals Ankle famous journals Ankle Google Scholar indexed journals Distal joints articles Distal joints Research articles Distal joints review articles Distal joints PubMed articles Distal joints PubMed Central articles Distal joints 2023 articles Distal joints 2024 articles Distal joints Scopus articles Distal joints impact factor journals Distal joints Scopus journals Distal joints PubMed journals Distal joints medical journals Distal joints free journals Distal joints best journals Distal joints top journals Distal joints free medical journals Distal joints famous journals Distal joints Google Scholar indexed journals Pelvis articles Pelvis Research articles Pelvis review articles Pelvis PubMed articles Pelvis PubMed Central articles Pelvis 2023 articles Pelvis 2024 articles Pelvis Scopus articles Pelvis impact factor journals Pelvis Scopus journals Pelvis PubMed journals Pelvis medical journals Pelvis free journals Pelvis best journals Pelvis top journals Pelvis free medical journals Pelvis famous journals Pelvis Google Scholar indexed journals Knee articles Knee Research articles Knee review articles Knee PubMed articles Knee PubMed Central articles Knee 2023 articles Knee 2024 articles Knee Scopus articles Knee impact factor journals Knee Scopus journals Knee PubMed journals Knee medical journals Knee free journals Knee best journals Knee top journals Knee free medical journals Knee famous journals Knee Google Scholar indexed journals Lower limb articles Lower limb Research articles Lower limb review articles Lower limb PubMed articles Lower limb PubMed Central articles Lower limb 2023 articles Lower limb 2024 articles Lower limb Scopus articles Lower limb impact factor journals Lower limb Scopus journals Lower limb PubMed journals Lower limb medical journals Lower limb free journals Lower limb best journals Lower limb top journals Lower limb free medical journals Lower limb famous journals Lower limb Google Scholar indexed journals Tibial plateau articles Tibial plateau Research articles Tibial plateau review articles Tibial plateau PubMed articles Tibial plateau PubMed Central articles Tibial plateau 2023 articles Tibial plateau 2024 articles Tibial plateau Scopus articles Tibial plateau impact factor journals Tibial plateau Scopus journals Tibial plateau PubMed journals Tibial plateau medical journals Tibial plateau free journals Tibial plateau best journals Tibial plateau top journals Tibial plateau free medical journals Tibial plateau famous journals Tibial plateau Google Scholar indexed journals Sagittal plane articles Sagittal plane Research articles Sagittal plane review articles Sagittal plane PubMed articles Sagittal plane PubMed Central articles Sagittal plane 2023 articles Sagittal plane 2024 articles Sagittal plane Scopus articles Sagittal plane impact factor journals Sagittal plane Scopus journals Sagittal plane PubMed journals Sagittal plane medical journals Sagittal plane free journals Sagittal plane best journals Sagittal plane top journals Sagittal plane free medical journals Sagittal plane famous journals Sagittal plane Google Scholar indexed journals Tibial glenoid cavities articles Tibial glenoid cavities Research articles Tibial glenoid cavities review articles Tibial glenoid cavities PubMed articles Tibial glenoid cavities PubMed Central articles Tibial glenoid cavities 2023 articles Tibial glenoid cavities 2024 articles Tibial glenoid cavities Scopus articles Tibial glenoid cavities impact factor journals Tibial glenoid cavities Scopus journals Tibial glenoid cavities PubMed journals Tibial glenoid cavities medical journals Tibial glenoid cavities free journals Tibial glenoid cavities best journals Tibial glenoid cavities top journals Tibial glenoid cavities free medical journals Tibial glenoid cavities famous journals Tibial glenoid cavities Google Scholar indexed journals Squat movement articles Squat movement Research articles Squat movement review articles Squat movement PubMed articles Squat movement PubMed Central articles Squat movement 2023 articles Squat movement 2024 articles Squat movement Scopus articles Squat movement impact factor journals Squat movement Scopus journals Squat movement PubMed journals Squat movement medical journals Squat movement free journals Squat movement best journals Squat movement top journals Squat movement free medical journals Squat movement famous journals Squat movement Google Scholar indexed journals Kinematic articles Kinematic Research articles Kinematic review articles Kinematic PubMed articles Kinematic PubMed Central articles Kinematic 2023 articles Kinematic 2024 articles Kinematic Scopus articles Kinematic impact factor journals Kinematic Scopus journals Kinematic PubMed journals Kinematic medical journals Kinematic free journals Kinematic best journals Kinematic top journals Kinematic free medical journals Kinematic famous journals Kinematic Google Scholar indexed journals
Article Details
Abbreviations
QMA: Quantified Motion Analysis
PiG: Plug In Gait
AoR: Axis of Rotation
CoR: Centre of Rotation
SCoRE: Symmetrical Centre of Rotation Estimation technique
SARA: Symmetrical Axis of Rotation Approach
OCST: Optimum Common Shape Technique
1. Introduction
Human movement has fuelled the thinking of scientists since Aristote's first observations. The walk represents, according to Carcreff et al [1], the most studied motor activity. It is indeed the most repeated movement and whose analysis is facilitated by its cyclical aspect. The evolution of technologies has made it possible to develop techniques for the study of movement, offering the possibility of quantifying gait according to different aspects: quantified motion analysis (QMA). This information will facilitate the identification and understanding of walking disorders and their causes for clinicians in order to improve the therapeutic recommendations according to DeLuca [2].
One of the key questions of this clinical examination is its reliability and the reproducibility of its results. According to Nair et al [3], precisely defining the articular centres is the prerequisite to guarantee the accuracy of the calculation of the kinematic and dynamic parameters during the QMA. Despite technical progress, there are errors inherent in calculation methods or models as well as in motion capture systems [4-6]. Della-Croce et al in 2005 [7] show that the calculation of articular centres is associated with errors due to the improper localization of skin markers, with inter-operator differences of up to 20mm, even in experienced operators. In addition, the relative movement between the markers and the underlying structures (soft tissue and bone) introduces errors which compromise the estimation of skeletal movement according to Peters et al [8].
2. Estimate of Joint Rotation Axes
The QMA is based on biomechanical principles. Indeed, for the study of movement, the human being is considered as a rigid poly-articulated mechanical system, supposed to be undeformable, which can be broken down into several bones segments. In three dimensions, a segment is associated with a reference frame defined by three non-collinear points: a coordinate system. The coordinate system has an orientation and a position. The principle of modeling is to associate a reference point with each anatomical segment of the body. It is from these reference frames that we can calculate the movements of translations and rotations of the segments. The Vicon® Plug-in-Gait (PiG) model, used in most gait analysis laboratories, is the reference method. It applies a so-called predictive method in the calculation of the Axis of Rotation (AoR) [9].
To determine the centre of rotation (CoR) of the hip, the PiG estimates it using three (or four) markers located on the pelvis, with a stationary subject. From the hip CoR and, thanks to other markers on the thigh, the PiG estimates the knee AoR [5], then according to an equivalent method, that of the ankle. Therefore, errors in the proximal joints are passed on to the distal joints.
This observation is all the more marked in subjects where bone markers are difficult to identify around the pelvis, for example in overweight subjects. Neptune and Hull as early as 1995 [10] show that the results of these predictive approaches for hip CoR have been found to be inaccurate by around 20 mm compared to radiographic measurements. More recently, in 2011, the work of Sangeux et al found an average error of 30 mm in the PiG compared to an X-ray analysis [11] or via a 3D ultrasound system [12].
3. Functional Method for Estimating Knee AoR
Chia and Sangeux explain in 2017 [13] that the measures of gait analysis are variable. The sources of variability can be intrinsic (between an individual's strides) or extrinsic. Extrinsic variability corresponds to the variability of the gait analysis measurement process, for example the replacement of markers between sessions and between assessors, or different marker placement protocols and treatment processes (such as estimates of axes and articular centers).
Leardini et al (1999) demonstrated that CoR and AoR can be determined more precisely by so-called functional methods [14], using joint mobility. The AdR are therefore determined independently of each other and are freed from the precision of the placement of the skin markers according to Schache and et al [15]. These techniques are distinguished in two categories as explained by Ehrig et al [16]:
- Spherical adjustment methods: where the joint is assimilated to a sphere in order to define CoR estimated by the trajectory of the markers [17, 18].
- Transformation techniques: like the Axis Transformation Technique [18, 19] or the Symmetrical Axis of Rotation Approach (SARA) [20].
The SARA transformation technique assumes that the AoR is mobile in the global coordinate system (represented by the calibration coordinate system). The two adjacent segments are therefore mobile in space which is closer to the reality of the movement. The philosophy of this technique is that the coordinates of the AoR remain constant with respect to the two segments throughout the movement. A local coordinate system is defined for each of the adjacent segments (thigh and leg for example). In each of these local systems, an AoR is defined. The SARA technique then allows the transformation into rotation and translation of the local coordinate systems towards the global coordinate system (Figure 1) thanks to calibration movements and thus allowing the definition of the global AoR of formula:
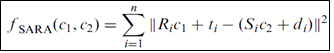
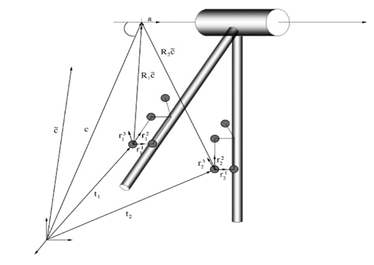
Figure 1: Diagram illustrating the construction of the coordinate systems and the axis of rotation of the knee from Ehrig and et al [20].
Several studies have shown the superiority in terms of reproducibility and reliability of functional methods compared to predictive methods in estimating joint centres, including that of Fiorentino et al [ 21] or Sangeux et al [11, 12]. Taylor et al [22] explained that transformation techniques gave more stable results than other techniques for estimating ADR in the context of the knee. However, the literature highlights the fact that all these methods remain subject to error due to skin movements. However, this error can be reduced by adding to functional techniques, an algorithm making it possible to reduce the noise of skin movements, such as, for example, the Optimal Common Shape Technique (OCST) introduced by Taylor et al in 2010 [22]. The functional methods to which the authors refer involve capturing the movement of the subject's lower limb as he explores most of the mobile capabilities of the joint. Several models of movements have been proposed and according to a study by Camomilla et al [19], it would seem that the “Star-arc” movement (star movement then circumduction) shows the best reproducibility to determine the hip CoR via the SCoRE method. To our knowledge, there are only few studies exploring the optimal calibration movement for the estimation of knee AoR.
If the literature tends to show that functional methods have a reproducibility advantage over predictive methods, there is no consensus on the positioning of knee AoR. There are some data proposing a mapping of marker placement [23, 24] but these combinations require a very precise placement of the markers (notably on anatomical landmarks) or a large number of markers, which is not suitable for clinical practice and could be deepened. Indeed, Besier et al (2003) [25] explain that functional techniques have better reproducibility in the definition of knee AoR, because it has the advantage of overcoming the precision of locating landmarks bony. This assertion is supported by the work of Sangeux [26] who finds in his 2018 study that the methods of functional knee calibration are significantly more reproducible than the conventional method between sessions of the same assessor. In a study published in 2016, Colle et al [27] compare several functional methods for estimating knee AoR and explain that the SARA transformation technique makes it possible to obtain the most stable and therefore most reproducible results. The choice of the use of this estimation technique is justified.
4. Calibration Movement
If the use of the SARA technique for the estimation of knee AoR finds justification in the literature, there does not seem to be a consensus as to the calibration movement that allows the best reproducibility of knee AoR to be obtained. The knee flexion movement between 0 and 20 ° of flexion essentially consists of the rotation of the femoral condyles on the tibial plateau on the sagittal plane. From 20 ° flexion, the translation is added to the rotation, but due to the non-symmetry of the femoral condyles and the tibial glenoid cavities, a medial rotation takes place in the transverse plane. The complexity of the knee flexion movement is therefore accentuated from 20 ° of flexion, thus modifying the instantaneous centres of rotation each time the amplitude changes. The definition of the AoR is therefore supposedly more difficult from this bending angle of 20 °.
It is easy to assume that larger movements could improve the accuracy and reproducibility of the estimate of knee AoR by the time it takes to travel it. The more time it takes to complete the movement, the longer it takes to measure, thus allowing more data to be collected. The same would apply if the instruction given to the subject was to perform a slow movement, but the variability in the realization of the calibration movement between individuals could compromise the reproducibility of the AoR estimate. In 2018, Sangeux [26] shows that functional calibration presents more reproducible results for predictive methods only when the knee flexion is greater than 20 ° but when the total range of motion is reduced (without specify the amplitude). However, Sangeux's study is done on a calibration during walking by varying during this initial angle of flexion of the knee.
In a 2014 work, Reichl and Ongaro [28] study different calibration movements to estimate the knee AoR via SARA: the squat movement, that from rowing and that from cycling. It turns out that the authors show that the squat movement between 35 and 65° of knee flexion gives the least stable results of the estimation of the AoR compared to other movements that study flexion movements between 60 and 90° of flexion. They attribute this difference to the fact that the squat is a free movement while the other two are machine-guided movements. The question of the value of using a guided movement to estimate the AoR of the knee before QGA may arise, but would increase the costs and the time taken for the examination. In clinical practice, there is the problem of the subjects' articular mobility and their ability to achieve the required movement. In fact, the quantified gait analysis is aimed at a population, whose gait may present deviations from physiology, including knee flexum or recurvatum. This work tends to show that the calibration movements allow greater reproducibility of the knee AoR if they start at 0 ° extension. What about patients who start the flexion movement from hyper-extension or who have lost total knee extension capacity. Human walking is made up of an alternating phase where the lower limb is in support and where it is in the air. The study of calibration movements is limited here to the closed chain that is to say that the subject's feet touch the ground, in a squat movement. The question of the interest of proposing calibration movements in open (or mixed) chain arises, in order to reproduce the so-called oscillating phase of walking as described by Passmore and Sangeux in 2016 [29] without mentioning the superiority of a such calibration movement in relation to the squat movement.
5. Conclusion
In QMA, kinematic and dynamic analysis is subject to the estimation of the centres and axes of rotation of the observed joints. This estimate must be as reproducible as possible so that clinically extrapolated data, such as kinematic values, make sense. In fact, the functional and predictive methods of estimating the centres and articular axes were created in asymptomatic subjects and do not take pathologies into account. It would be interesting to compare the estimation of the axes of rotation by these different methods in subjects suffering from arthritis pathology. The definition of the axis of rotation of the knee would also make it possible to know, for the patients having benefited from a knee arthroplasty, if the surgical technique allows the restoration of the functional axis of mobility or not, explaining the painful clinic sometimes persistent. The literature has fixed a threshold for error in the location of the hip joint centre at 30 mm, beyond which there is significant inaccuracy in the estimation of the hip joint centre [21]. The literature has not yet revealed the existence of such a threshold of imprecision applicable to the knee joint.
References
- Carcreff L, Bonnefoy-Mazure A, De Coulon G, et al. Analyse quantifiée de la marche. Mov Sport Sci - Sci Mot (2016): 7-21.
- DeLuca PA, Davis RB, Ounpuu S, et al. Alterations in surgical decision making in patients with cerebral palsy based on three-dimensional gait analysis. J Pediatr Orthop 17 (1997): 08-14.
- Nair SP, Gibbs S, Arnold G, et al. A method to calculate the centre of the ankle joint: A comparison with the Vicon® Plug-in-Gait model. Clin Biomech 25 (2010): 582-587.
- Carcreff L, Bonnefoy-Mazure A, De Coulon G, et al. Analyse quantifiée de la marche. Mov Sport Sci - Sci Mot (2016): 7-21.
- Nair SP, Gibbs S, Arnold G, et al. A method to calculate the centre of the ankle joint: A comparison with the Vicon® Plug-in-Gait model. Clin Biomech 25 (2010): 582-587.
- Schwartz MH, Trost JP, Wervey RA. Measurement and management of errors in quantitative gait data. Gait Posture 20 (2004): 196-203.
- Della Croce U, Leardini A, Chiari L, et al. Human movement analysis using stereophotogrammetry. Gait Posture 21 (2005): 226-237.
- Peters A, Galna B, Sangeux M, et al. Quantification of soft tissue artifact in lower limb human motion analysis: A systematic review. Gait Posture 31 (2010): 1-8.
- Vicon Nexus User Guide n.d.: 209.
- Neptune RR, Hull ML. Methods for Determining Hip Movement in Seated Cycling and Their Effect on Kinematics and Kinetics. J Appl Biomech 12 (1996): 493-507.
- Sangeux M, Pillet H, Skalli W. Which method of hip joint centre localisation should be used in gait analysis? Gait Posture 40 (2014): 20-25.
- Sangeux M, Peters A, Baker R. Hip joint centre localization: Evaluation on normal subjects in the context of gait analysis. Gait Posture 11 (2011): 324-328.
- Chia K, Sangeux M. Quantifying sources of variability in gait analysis. Gait Posture 56 (2017): 68-75.
- Leardini A, Cappozzo A, Catani F, et al. Validation of a functional method for the estimation of hip joint centre location. J Biomech 32 (1999): 99-103.
- Schache AG, Baker R, Lamoreux LW. Defining the knee joint flexion-extension axis for purposes of quantitative gait analysis: An evaluation of methods. Gait Posture24 (2006): 100-109.
- Ehrig RM, Taylor WR, Duda GN, et al. A survey of formal methods for determining the centre of rotation of ball joints. J Biomech 39 (2006): 2798-2809.
- Gamage SSHU, Lasenby J. New least squares solutions for estimating the average centre of rotation and the axis of rotation. J Biomech 35 (2002): 87-93.
- Halvorsen K. Bias compensated least squares estimate of the center of rotation. J Biomech 36 (2003): 999-1008.
- Camomilla V, Cereatti A, Vannozzi G, et al. An optimized protocol for hip joint centre determination using the functional method. J Biomech 39 (2006): 1096-1106.
- Ehrig RM, Taylor WR, Duda GN, et al. A survey of formal methods for determining functional joint axes. J Biomech 40 (2007): 2150-2157.
- Fiorentino NM, Kutschke MJ, Atkins PR, et al. Accuracy of Functional and Predictive Methods to Calculate the Hip Joint Center in Young Non-pathologic Asymptomatic Adults with Dual Fluoroscopy as a Reference Standard. Ann Biomed Eng 44 (2016): 2168-2180.
- aylor WR, Kornaropoulos EI, Duda GN, et al. Repeatability and reproducibility of OSSCA, a functional approach for assessing the kinematics of the lower limb. Gait Posture 32 (2010): 231-236.
- Wen Y, Huang H, Yu Y, et al. Effect of tibia marker placement on knee joint kinematic analysis. Gait Posture 60 (2018): 99-103.
- Yin L, Chen K, Guo L, et al. Identifying the Functional Flexion-extension Axis of the Knee: An In-Vivo Kinematics Study. Plos one 10 (2015): e0128877.
- Besier TF, Sturnieks DL, Alderson JA, et al. Repeatability of gait data using a functional hip joint centre and a mean helical knee axis. J Biomech 36 (2003): 1159-1168.
- Sangeux M. Computation of hip rotation kinematics retrospectively using functional knee calibration during gait. Gait Posture 63 (2018): 171-176.
- Colle F, Lopomo N, Visani A, et al. Comparison of three formal methods used to estimate the functional axis of rotation: an extensive in-vivo analysis performed on the knee joint. Comput Methods Biomech Biomed Engin 19 (2016): 484-492.
- Reichl I, Ongaro M. Finite helical axis versus symmetrical axis of rotation approach for the human knee joint: squats, rowing and cycling. Comput Methods Biomech Biomed Engin 16 (2013): 109-111.
- Passmore E, Sangeux M. Defining the medial-lateral axis of an anatomical femur coordinate system using freehand 3D ultrasound imaging. Gait Posture 45 (2016): 211-216.
