Fluid-Structure Interaction Simulation of Artificial Heart Valve Considering Open State of Cardiac Cycle
Article Information
Shahrul Hisyam Marwan1, 2, Mitsugu Todo1, 3
1Department of Molecular and Material Sciences, Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, Fukuoka, Japan.
2School of Mechanical Engineering, College of Engineering, Universiti Teknologi MARA, Terengganu Branch, Bukit Besi Campus, Terengganu, Malaysia.
3Research Institute for Applied Mechanics, Kyushu University, Fukuoka, Japan.
*Corresponding Author: Mitsugu Todo, Associate Professor, Research Institute for Applied Mechanics, Kyushu University, 6-1 Kasuga-koen, Kasuga, Fukuoka 816-8580, Japan
Received: 11 July 2021; Accepted: 20 July 2021; Published: 30 July 2021
Citation:
Shahrul Hisyam Marwan, Mitsugu Todo. Fluid-Structure Interaction Simulation of Artificial Heart Valve Considering Open State of Cardiac Cycle. Journal of Biotechnology and Biomedicine 4 (2021): 124-131.
View / Download Pdf Share at FacebookAbstract
The dynamic finite element method with the fluid-structure interaction was used to investigate the deformation behavior of a newly developed artificial heart valve. To reproduce the opening movements of tri-leaflets of the valve during the half cardiac cycle, a time-dependent blood velocity was used as the boundary condition of the fluid domain. The nonslip boundary condition was also chosen for the tri-leaflets to ensure the viscous effect between the blood and the leaflet surfaces, while the free slip boundary condition was chosen for the cylindrical wall to ignore such viscous effect. The valve was assumed to be made from a natural tissue and a linear elastic material was assumed as the material model. The blood was assumed to be incompressible and Newtonian fluid. It was found that the valve was easily open when it came into contact with blood flow, taking only 0.3 seconds to go from fully closed to fully open. The blood flow was also found to be stable with a laminar state and free of turbulence.
Keywords
Artificial heart valve; Fluid-structure interaction; Dynamic finite element method; Solid domain; Fluid domain; Cardiac cycle
Artificial heart valve articles Artificial heart valve Research articles Artificial heart valve review articles Artificial heart valve PubMed articles Artificial heart valve PubMed Central articles Artificial heart valve 2023 articles Artificial heart valve 2024 articles Artificial heart valve Scopus articles Artificial heart valve impact factor journals Artificial heart valve Scopus journals Artificial heart valve PubMed journals Artificial heart valve medical journals Artificial heart valve free journals Artificial heart valve best journals Artificial heart valve top journals Artificial heart valve free medical journals Artificial heart valve famous journals Artificial heart valve Google Scholar indexed journals Fluid-structure interaction articles Fluid-structure interaction Research articles Fluid-structure interaction review articles Fluid-structure interaction PubMed articles Fluid-structure interaction PubMed Central articles Fluid-structure interaction 2023 articles Fluid-structure interaction 2024 articles Fluid-structure interaction Scopus articles Fluid-structure interaction impact factor journals Fluid-structure interaction Scopus journals Fluid-structure interaction PubMed journals Fluid-structure interaction medical journals Fluid-structure interaction free journals Fluid-structure interaction best journals Fluid-structure interaction top journals Fluid-structure interaction free medical journals Fluid-structure interaction famous journals Fluid-structure interaction Google Scholar indexed journals Dynamic finite element method articles Dynamic finite element method Research articles Dynamic finite element method review articles Dynamic finite element method PubMed articles Dynamic finite element method PubMed Central articles Dynamic finite element method 2023 articles Dynamic finite element method 2024 articles Dynamic finite element method Scopus articles Dynamic finite element method impact factor journals Dynamic finite element method Scopus journals Dynamic finite element method PubMed journals Dynamic finite element method medical journals Dynamic finite element method free journals Dynamic finite element method best journals Dynamic finite element method top journals Dynamic finite element method free medical journals Dynamic finite element method famous journals Dynamic finite element method Google Scholar indexed journals Solid domain articles Solid domain Research articles Solid domain review articles Solid domain PubMed articles Solid domain PubMed Central articles Solid domain 2023 articles Solid domain 2024 articles Solid domain Scopus articles Solid domain impact factor journals Solid domain Scopus journals Solid domain PubMed journals Solid domain medical journals Solid domain free journals Solid domain best journals Solid domain top journals Solid domain free medical journals Solid domain famous journals Solid domain Google Scholar indexed journals Fluid domain articles Fluid domain Research articles Fluid domain review articles Fluid domain PubMed articles Fluid domain PubMed Central articles Fluid domain 2023 articles Fluid domain 2024 articles Fluid domain Scopus articles Fluid domain impact factor journals Fluid domain Scopus journals Fluid domain PubMed journals Fluid domain medical journals Fluid domain free journals Fluid domain best journals Fluid domain top journals Fluid domain free medical journals Fluid domain famous journals Fluid domain Google Scholar indexed journals Cardiac cycle articles Cardiac cycle Research articles Cardiac cycle review articles Cardiac cycle PubMed articles Cardiac cycle PubMed Central articles Cardiac cycle 2023 articles Cardiac cycle 2024 articles Cardiac cycle Scopus articles Cardiac cycle impact factor journals Cardiac cycle Scopus journals Cardiac cycle PubMed journals Cardiac cycle medical journals Cardiac cycle free journals Cardiac cycle best journals Cardiac cycle top journals Cardiac cycle free medical journals Cardiac cycle famous journals Cardiac cycle Google Scholar indexed journals asymmetry articles asymmetry Research articles asymmetry review articles asymmetry PubMed articles asymmetry PubMed Central articles asymmetry 2023 articles asymmetry 2024 articles asymmetry Scopus articles asymmetry impact factor journals asymmetry Scopus journals asymmetry PubMed journals asymmetry medical journals asymmetry free journals asymmetry best journals asymmetry top journals asymmetry free medical journals asymmetry famous journals asymmetry Google Scholar indexed journals 3D model articles 3D model Research articles 3D model review articles 3D model PubMed articles 3D model PubMed Central articles 3D model 2023 articles 3D model 2024 articles 3D model Scopus articles 3D model impact factor journals 3D model Scopus journals 3D model PubMed journals 3D model medical journals 3D model free journals 3D model best journals 3D model top journals 3D model free medical journals 3D model famous journals 3D model Google Scholar indexed journals cardiovascular articles cardiovascular Research articles cardiovascular review articles cardiovascular PubMed articles cardiovascular PubMed Central articles cardiovascular 2023 articles cardiovascular 2024 articles cardiovascular Scopus articles cardiovascular impact factor journals cardiovascular Scopus journals cardiovascular PubMed journals cardiovascular medical journals cardiovascular free journals cardiovascular best journals cardiovascular top journals cardiovascular free medical journals cardiovascular famous journals cardiovascular Google Scholar indexed journals artificial heart articles artificial heart Research articles artificial heart review articles artificial heart PubMed articles artificial heart PubMed Central articles artificial heart 2023 articles artificial heart 2024 articles artificial heart Scopus articles artificial heart impact factor journals artificial heart Scopus journals artificial heart PubMed journals artificial heart medical journals artificial heart free journals artificial heart best journals artificial heart top journals artificial heart free medical journals artificial heart famous journals artificial heart Google Scholar indexed journals
Article Details
1. Introduction
Computational simulation techniques have been an important tool for understanding the interaction between artificial aortic heart valves and blood flow. For example, the finite element method (FEM) with the fluid–structure interaction (FSI) has effectively been utilized to simulate the dynamic motion of a heart valve throughout the cardiac cycle [1, 2]. It is however difficult to analyze the hemodynamic performance of blood flow under the strong interaction between the valve and blood flow in the FEM-FSI modeling. To overcome this problem, a precise 3D model of the valve should be created, and the valve's specific properties must be incorporated into the FEM-FSI analysis. In addition, in order to characterize the opening behavior of the valve correctly, the blood flow in the vicinity of the valve must be analyzed. The fluid and structural models have successfully evolved in a couple of simulation systems to accurately represent these interactions, and the accuracy has dramatically been improved.
The aim of this research was to construct a 3D FSI model of a newly developed artificial heart valve with three leaflets taking blood flow into account. To analyze the deformation of the leaflets, the dynamic finite element analysis was used to examine the open response of the valve during the interaction with blood flow by simulating a half cardiac cycle. The hemodynamic behavior of blood flow during the interaction with the valve was also examined in this study.
2. Modeling
2.1 Solid domain
A 3D CAD model of an artificial heart valve was created using a free computer-aided design software Fusion 360 (Autodesk, Inc.), by referring to the substantial details of the geometry provided by Gharaie and Morsi [3]. The external appearances of the 3D model with asymmetric tri-leaflet are shown in Figure 1. The height, diameter and thickness of the 3D model are 8.5, 25.0 and 0.5 mm, respectively [3]. The finite element meshes were created after the 3D model was exported to the finite element code LS-DYNA (Liverware Software, Livermore, CA). The 3D aortic valve was modelled with 17961 tetrahedral solid elements and 6302 nodes as shown in Figure 2. The valve was assumed to be made of a biological tissue used in standard bio-prosthetic heart valves. The density, Young’s modulus, and the Poisson’s ratio were then set to be 1,100 kg/m3 [4–6], 1.0 MPa [4, 7], and 0.3 [4, 8], respectively.
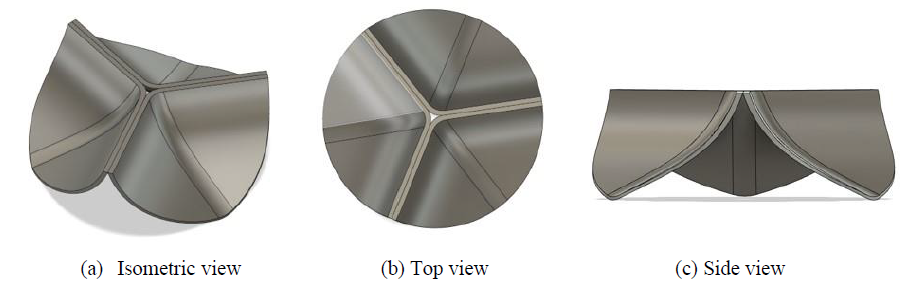
Figure 1: External appearances of artificial heart valve with asymmetric tri-leaflet.

Figure 2: Finite element model of artificial heart valve.
2.2 Fluid domain
The fluid was assumed to be contained in a pipe-like shell structure surrounding the asymmetry tri-leaflets aortic valve model. A 3D CAD model of the fluid domain was created using the 3D-CAD Fusion 360. The length and diameter of the shell structure were 40.0 and 23.5 mm, respectively. The 3D pipe-like shell model with the tri-leaflet valve model are shown in Figure 3. The geometrical data were transferred to LS-DYNA and the finite element meshes were constructed. The fluid domain was discretized with tetrahedral elements, and the pipe-like shell was modelled with 36472 surface elements and 18238 surface nodes, as shown in Figure 4. The fluid was assumed to be incompressible and Newtonian [9], with a constant dynamic viscosity of 0.004 kg/m-s [3, 10] and a density of 1060 kg/m3 [11, 12]

Figure 3: 3D model of pipe-like shell with a tri-leaflet valve.

Figure 4: Finite element meshes of fluid domain.
2.3 Boundary conditions
All nodes along the side edges of the asymmetry leaflets were fixed in all directions as the geometrical boundary condition. The fluid domain had two boundaries, namely, inlet and outlet, as shown in Figure 5. The prescribed velocity boundary condition was set on the inlet part to simulate clinically relevant blood flow, while the prescribed pressure boundary condition was set on the outlet with a value of zero to express a continuous flow. An acceleration of 110 mm/s2 was given to the flow to simulate the blood flowing through the aortic valve in our cardiovascular system, starting zero velocity at t = 0 s, and a uniform fluid stream entered the inlet from the left. To express a viscous effect of blood, the nonslip boundary condition was set on the surfaces of the tri-leaflets to ensure the viscous effect between the blood and the leaflets surface, while the free slip boundary condition was given to the cylindrical wall to ignore the viscous effect between the blood and the cylindrical wall.
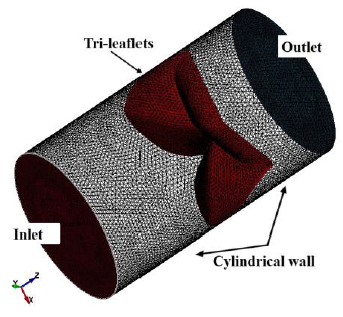
Figure 5: Boundaries of fluid domain.
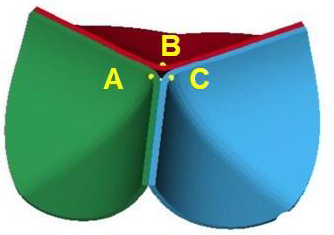
Figure 6: Three points on the tri-leaflets.
3. Results and Discussion
3.1 Dynamic deformation behavior of the artificial heart valve
In this FEM-FSI analysis, the opening behavior of the aortic valve due to the blood flow was successfully observed. The total displacements were measured at the three points on the tri-leaflets shown in Figure 6. The time histories of the displacements are shown in Figure 7 (a). The displacements are almost equivalent, suggesting that the opening behavior of the tri-leaflets are totally symmetric. The displacements at three points are also shown at t=0.4 s in Figure 7 (b). Although the differences are very small, the displacement of the node C was biggest, affecting the hemodynamics of the fluid discussed later.
The deformed images observed from the front view at four different times (points (a)-(d) in Figure.7) are also shown in Figure 8. The valve started to open just before t = 0.1 s without any deformation at point (a). The valve then began to open at t = 0.2 s, resulting in a displacement of 0.26 mm at point (b), and fully opened at t = 0.4 s, resulting in a displacement of 7.60 mm at point (d). It can be seen that the valve demonstrated rapid opening behavior from the point (c) to (d), with the valve's rate of displacement approaching 68 mm/s as shown in Figure 9. This unnatural deformation behavior may be related to the buckling of the linear elastic shell structure
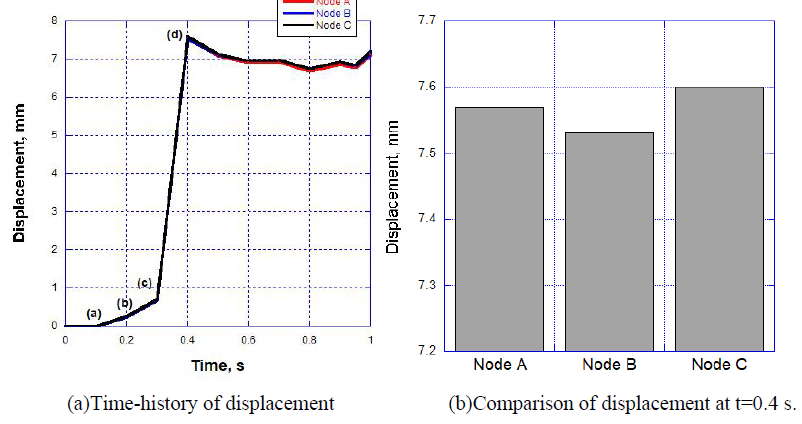
Figure 7: Resultant displacement data at three points.
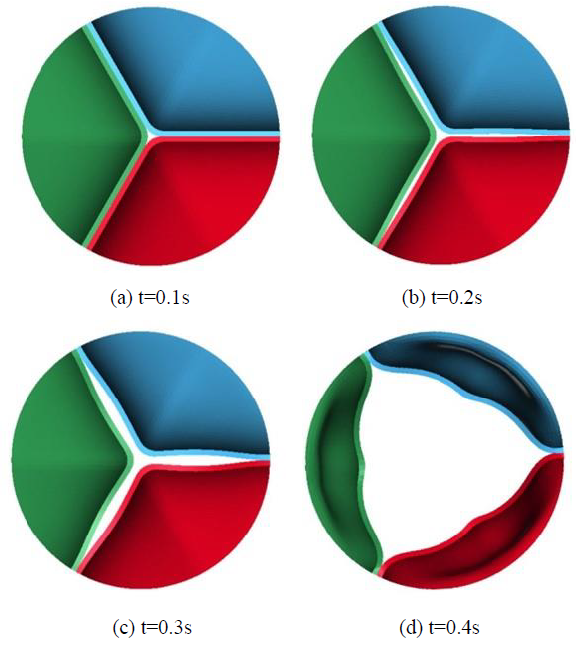
Figure 8: Deformation behaviors of the leaflets.
3.2 Hemodynamic behavior during opening state of artificial heart valve
The hemodynamics of blood flowing through the opening valve was also examined from the results of the FEM-FSI analysis. The fluid velocity vectors are shown in Figure 10 at three different times corresponding to the points (b), (c) and (d) in Figures 8 and 9. The maximum fluid velocity was 362.7 mm/s at t=0.2 s and occurred at the center of the valve, while at t=0.4 s when the valve was fully open, the maximum fluid velocity was 536.5 mm/s and occurred at the slight right-hand location of the center, as shown in Figure 10 (c). This kind of inclination may be related to the unsymmetrical deformation of the leaflets of the valve. As shown in Figure 7 (b), the node C exhibited the largest displacement, indicating that the opening behavior of the leaflet including the node C showed the widest. Actually, the direction of the maximum velocity vector coincided with the direction from the center toward the node C.
The Reynolds numbers evaluated from the maximum velocities at t=0.2 and 0.4 s were Re = 2256 and 3341, respectively, and corresponded to a laminar (Re ≤ 2,300) and transient flow (2,300 < Re < 4000), and no turbulent flow took place in this simulation.
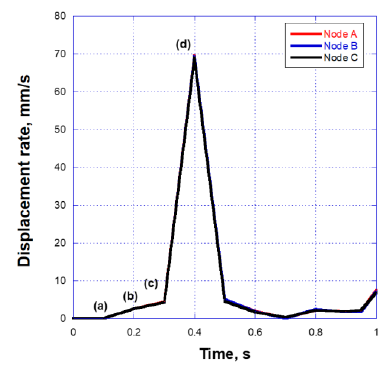
Figure 9: Displacement at the three points shown in Fig.6.

Figure 10: 2D fluid velocity vectors passed through the valve.
4. Conclusions
The FEM-FSI method was successfully used to analyze the dynamic deformation behavior of a newly developed artificial bio-prosthetic heart valve installed in a pipe-like shell structure with blood flow. The opening state of the valve's tri-leaflets was successfully simulated during the half cardiac cycle. It was found that when the valve comes into contact with blood flow, it opens quickly, taking only 0.3 seconds to go from fully closed to fully open state. It was also found that the blood flow was stable and turbulence-free. It was thus concluded that the blood flow is crucial in ensuring that the artificial valve can be opened easily with a laminar flow condition.
References
- AP Yoganathan, KB Chandran, F Sotiropoulos. “Flow in prosthetic heart valves: State-of-the-art and future directions,” Annals of Biomedical Engineering 33 (2005): 1689-1694.
- JH Lee, AD Rygg, EM Kolahdouz, et al. “Fluid–Structure Interaction Models of Bioprosthetic Heart Valve Dynamics in an Experimental Pulse Duplicator,” Annals of Biomedical Engineering 48 (2020): 1475-1490.
- SH Gharaie, Y Morsi. “A novel design of a polymeric aortic valve,” International Journal of Artificial Organs 38 (2015): 259-270.
- R Gnyaneshwar, RK Kumar. “Original article: cardiovascular Dynamic analysis of the aortic valve using a finite” 73 (2002): 3-6.
- M Thubrikar, “The aortic valve,” CRC Press, Boca Raton,Florida (1990): 11-20.
- M Abbasi, MS Barakat, K Vahidkhah, et al. “Characterization of three-dimensional anisotropic heart valve tissue mechanical properties using inverse finite element analysis,” Journal of the Mechanical Behavior of Biomedical Materials 62 (2016): 33-44.
- H Kim, J Lu, MS Sacks et al. “Dynamic simulation pericardial bioprosthetic heart valve function,” Journal of Biomechanical Engineering 128 (2006): 717-724.
- AN Smuts, DC Blaine, C Scheffer, et al. “Application of finite element analysis to the design of tissue leaflets for a percutaneous aortic valve,” Journal of the Mechanical Behavior of Biomedical Materials 4 (2011): 85-98.
- A Vazifehdoostsaleh, M Darjani, A. Bahmani. “Engineering Solid Mechanics” 8 (2020): 271-284.
- CJ Cengel YA, Fluid Mechamics: Fundamentals and Application, Forth Edit (2018).
- CJ Carmody, G Burriesci, IC Howard, et al. “An approach to the simulation of fluid-structure interaction in the aortic valve,” Journal of Biomechanics 39 (2006): 158-169.
- I Borazjani. “Fluid-structure interaction, immersed boundary-finite element method simulations of bio-prosthetic heart valves,” Computer Methods in Applied Mechanics and Engineering 257 (2013): 103-116.
