Introduction

The amyloid forms of proteins with specific biological functions are an object of analysis due to their non-toxic presence in the living organism [1-4]. The peculiarity of toxic amyloid fibrils is their unrestricted propagation in the form of linear fibril structures disrupting the structure of cells and cell organelles, leading to pathological phenomena [5-10]. Particular attention is directed at proteins that perform their biological roles despite representing an amyloid-specific structure. An overview of such examples is given in a paper that lists the types of activity of proteins defined as functional amyloids [11]. The specificity of amyloid structure is as follows: the high presence of β-structure engaging a significant part of the chain in a network of hydrogen bonds with neighbouring chains. The vast majority of amyloids represent a parallel chain arrangement. The engagement, in many cases, of almost the entire chain length in a β-structure arrangement with an inter-chain system of hydrogen bonds results in a flat, 2D structure. The dominant feature is the possibility of unrestricted propagation of a linear fibril posing a threat to cell structures or intracellular organelles. The high number of hydrogen bonds results in high amyloid fibril stability [12]. Neurodegenerative amyloids identified in patient tissues show the presence of mutations [13-15]. In general, however, it is not known why these structures appear. Amyloid structures as highly ordered structures are also juxtaposed with the extreme form, that is, intrinsically disordered proteins [16]. It turns out that these structures, extreme from the point of view of ordering (especially in relation to globular structures), exhibit specific biological functions. An overview of curli amyloid proteins and their significant biological roles is discussed in detail in [4, 17-19]. However these proteins are not classified as emyloids using the model presented in this paper as the criterion for amyloid classification which is the possibility to propagate in unfinit scale.

Experimentally, numerous proteins can undergo amyloid transformation by means of shaking [20, 21]. A model of such transformation has been proposed as a process occurring in the air-water interface region [22]. Studies of this phenomenon concentrate on the structural analysis of water molecules under natural but also experimentally altered conditions [23-43]. A special subject matter is the analysis of the structuring of water in contact with a hydrophobic surface. [44,45]. The protein structure referred to as the “intelligent micelle” refers to proteins that show the presence of a centric hydrophobic core in their globular structure (compared to micelle) [46]. It is assumed that the distribution of hydrophobicity in a micelle can be expressed using a 3D Gaussian function. This is based on a model called fuzzy oil drop (FOD). The sequence of amino acids in the polypeptide chains of proteins, encoded by evolution, makes it possible to reproduce micelle-like structuring to a full or limited extent. A chain representing the correct proportion (and sizes) of hydrophobic to hydrophilic residues can fully recreate a micelle-like arrangement with a centric hydrophobic core and a polar surface. A local mismatch towards distribution in the form of a local deficit or local excess of hydrophobicity results in the appearance of a cavity used to bind ligands or substrates in the case of enzymes. Local exposure creates conditions for complexation of another protein, forming complexes. Proteins that do not show the presence of a hydrophobic core with a uniform distribution of hydrophobicity throughout the protein body require a non-aqueous environment for the folding process. The specificity of this environment is determined by the FOD-M model that takes into account the modification of the polar aqueous environment. This is expressed by the K parameter . The higher its value, the more altered the aqueous environment and the less marked the presence of hydrophobic nuclei in the protein [47-50]. Amyloid protein analysis based on the FOD model has been carried out for numerous proteins. The set of protein structures defined as pathological also includes proteins that play biological roles.

Amyloid proteins performing biological roles were analysed in the present study using the FOD-M model to indicate differences in their characteristics relative to known pathological amyloids.

Materials and Methods

Data

An analysis of the problem of amyloid fibril structure is discussed using the example of a functional amyloid, endorphin, whose structure is available in PDB - ID 6TUB [51] and a pathological amyloid, A-β ‘Osaka’, mutation E22Δ (PDB ID - 2MVX) [52]. For both amyloids analysed, fibrils built from 24 chains were constructed respecting the rules of mutual orientation of consecutive peptides according to the available structures in the PDB. The structures of the single chain and subsequent fibrils, which include one more chain, were analysed. Each successive step in the construction of the final fibril was analysed using the FOD-M model (described below), which assesses how hydrophobicity distributions are ordered in successive fibrils of increasing composition.

Description of the model used

The FOD model and its modified version (FOD-M) have been described in numerous papers [47]. Here, the model is briefly presented to facilitate result interpretation. It is assumed that the polar water environment directs the folding process toward the generation of a hydrophobic core with a polar surface. Such a structure is referred to as micelle-like. The hydrophobicity level of such an idealised system is expressed, at the effective atom position (the averaged position of the atoms comprising a given amino acid), as the value of a 3D Gaussian function spanning the entire body of the protein. The value of this idealised hydrophobicity level represented by particular effective atom (averaged position of atoms belonging to a particular amino acid) is referred to as Ti (theoretical) representing the T distribution (eq. 1.).

Eq 1

Parameters σ_x, σ_y and σ_z  are the Gauss function parameters expressing the size and shape of the protein molecule. The value 3xσ (for any direction) expresses the maximal distance versus the center (according to three sigma rule). The actual hydrophobicity level of a given amino acid (represented by an effective atom) is the result of intrinsic hydrophobicity (any scale can be used) and the strength of hydrophobic interaction with surrounding amino acids. This interaction is determined using functions proposed by Levitt [53].

Eq 2

The value of the actual state of a given amino acid is referred to as O_i (observed) to represent the O distribution.

Both distributions: T and O can be compared after normalisation of both of them. The comparison of the two distributions is assessed using the divergence entropy introduced by Kullback-Leibler, referred to as D_KL, for the relationship of the observed O distribution to the reference distribution T [54].

Eq 3

The D_KL value is a measure of entropy; therefore, a second reference distribution Ri is introduced, where all effective atoms represent the same undifferentiated level of hydrophobicity (Ri=1/N, where N is the number of amino acids in the polypeptide chain). A protein with the O distribution described by D_KL(O|T) < D_KL(O|R) is treated as representing a structure with a hydrophobic core. Otherwise, the structure of a given protein does not show a centric concentration of hydrophobicity. The degree of the O distribution’s closeness to/distance from the reference distribution T is expressed by relative distance (RD) expressing the ratio:

Eq 4

In this arrangement, if a protein is described by an RD < 0.5, this means identification of a protein with a hydrophobic core present. Since the aqueous environment is not the only environment for protein activity, a modification of the function expressing the distribution of hydrophobicity in the protein was introduced by adding an appropriate portion of a function complementary to the 3D Gaussian function (1-3DG). This function is the result of analysis of the specificity of the cell membrane environment, where, in contrast to the aqueous environment, hydrophobic residues are expected to be exposed on the surface for favourable interaction with the hydrophobic membrane. In the centre, however, a low hydrophobicity level is expected in a transmembrane protein acting as a channel for the transport of numerous molecules. Therefore, the inverse Gaussian function is assumed to represent the expected distribution of hydrophobicity in a membrane protein.

The following function is used to describe the hydrophobicity distribution in the FOD-M model:

Mi = 3DG_n + [K*(T_max-3DG)_n]_n            eq. 5.

where the index “n” denotes normalisation.

The value of the K parameter determines the degree to which the 3DG field, constituting the result of the external force field of the aqueous environment, is modified (weakened) by the contribution of the opposite to polar field of water.

Therefore, each protein discussed in the present work is evaluated using these parameters: RD and K. The RD value denotes the degree of matching/mismatching of the hydrophobicity distribution to the idealised system in a 3D Gaussian form (centric concentration of hydrophobicity with a polar surface). The parameter K value indicates the degree of modification of the external force field against the force field generated by polar water.

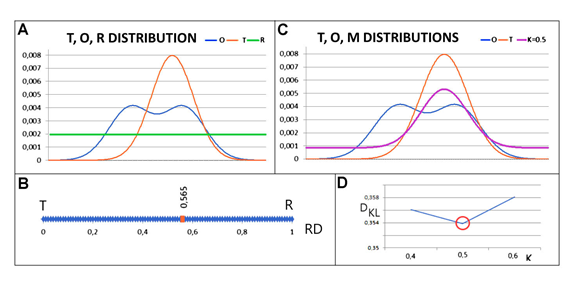
The graphical presentation of the FOD-M model illustrates the basis of the model:

Figure 1: Graphical presentation of the FOD-M model

A – idealised reference distribution T (red) expressing the Gauss function (in the model applied to proteins it is the 3D Gauss function), observed distribution O (blue) calculated using the eq. 2. (this calculation expressed all inter-residual interactions in protein) and reference distribution R (green) the second reference distribution deprived of any form of hydrophobicity differentiation in protein body.

B – RD value for the above-mentioned example distributions (eq. 4) – red dot, RD = 0.565 classifies status as deprived of hydrophobic (reduced to one dimension for simplicity)

C – summary of distributions T (orange) – the Gauss function (eq. 1.), O (blue) – inter-residual interactions (eq. 2.) and M (purple) (eq. 5) for the determined optimal value of the K parameter.

D – procedure for determining the K value – the value for the description of a given distribution O is determined for the minimum D_KL value for the (O|M) relationship (distinguished by the red circle). This means that the distribution of O was obtained by adapting to the distribution of M, which, with a force of K=0.5, was modified in relation to the Gaussian function.

The interpretation of the model based on Fig. 1 is as follows: three profiles: 1. T – theoretical, consistent with the 3D Gaussian function (hydrophobic core present); 2. O – distribution of observed hydrophobicity being the result of inter-residual interaction (Fig. 1.A). 3. In addition, there is the R distribution expressing a uniform distribution of hydrophobicity levels (hydrophobic core absent) (Fig.1.A). Comparison of the distributions expressed by RD=0.565 (Fig. 1.B) indicates the absence of a hydrophobic core due to RD > 0.5 (Fig. 1.B). The RD parameter takes values from the range of 0–1. The positioning of the calculated RD value indicates the similarity of the O distribution to the R distribution. The O distribution represents the status deprived of a hydrophobic core. The application of eq. 5 to the example in question indicates the M distribution for the value of the K parameter =0.5 (Fig. 1.C). The method of identifying the distribution of M is based on finding the minimum value of D_KL(O|M) for the optimal K value. Fig. 1.D shows the value of K=0.5 as satisfying the condition of minimum D_KL(O|M). Minimal D_KL(O|M) identifies the M distribution as the most similar with respect to the O distribution. The folding chain – as it is interpreted – was adapting its structure to the external force field (function M) during the folding process.

The FOD-M model was applied in this work to assess the structure of single chains and fibrils with a step-wise increasing number of chains in the fibril.

Results

Analysis of pathological fibril – A-β ‘Osaka’

The A-β 'Osaka' amyloid with the E22Δ mutation was chosen as an example of a pathological fibril (PDB ID – 2MVX [52]). This amyloid is available as a super-fibril with two proto-fibrils. This is why the analysis for proto-fibril and for super-fibril is presented.

The change in RD and K parameter values for increasing proto-fibril length is shown in Fig. 2.A.

Figure 2: Characterisation of the growing (an increasing number of chains in the fibril) proto-fibril of the A-β ‘Osaka’ amyloid with the E22Δ mutation.

A - change in RD (blue) and K (red) for increasing number of chains (horizontal axis). Green line - RD=0.5 level - the threshold adopted to identify a micelle-like system (RD < this level indicates a system with a centric hydrophobic nucleus present together with a polar surface).

B - variation of the sigmaX (blue), SigmaY(red) and SigmaZ (green) parameters with increasing number of chains in the proto-fibril.

C - 3D form of a 24-chain proto-fibril generated based on the geometry of a 5-chain fibril available in PDB with a single-chain (red) highlighted

D - form of the five-chain fibril - the length was chosen based on the values of the RD and K parameters closest to the micelle-like system

E - summary of profiles T (blue), O (red) and M (green) for K=1.7 to illustrate the characteristics of a proto-fibril with 24 chains.

F - set of profiles: T (blue), O (red) and M (green) for K=0.7. A set of five chains was selected as in (C) above, based on the minimum values of the RD andf K parameters.

A comparative analysis of the profiles (Fig. 2.(A) suggests a status far from a micelle-like arrangement for the A-β ‘Osaka’ fibril regardless of the composition of the fibril and, therefore, its length. The status of highest agreement with the distribution expressed by the 3D Gaussian function shows a five-chain composition, although this status does not correspond to a micelle-like structuring. The RD values are above 0.5 for all fibril lengths with minimum values of K = 0.7. In the interpretation of the FOD-M model, this means that the stability of this system requires environmental conditions that are altered with respect to the aqueous environment to the extent expressed by K. This is related to the change in conditions that is observed in the experiment due to shaking of the solution containing the protein in question. An RD value > 0.5 and an elevated K parameter value indicate the need to stabilise the fibril of the protein in a environment modified relative to an aqueous solution. Analysis of the geometry of a fibril with an increasing number of chains does not reveal a spherical arrangement, representing divergent values of the SigmaX, SigmaY and SigmaZ parameters at each fibril length (Fig. 2.B).

Fig. 2.C is a visualisation of a 24-chain proto-fibril reconstructed with geometrical relationships AND mutual orientation consistent with the arrangement present in the 5-chain structure available in PDB. A single chain is shown in red. Fig. 2.D is a visualisation of a 5-chain arrangement, which represents the status closest to the micelle-like system (Fig. 2.A and B) considering the hydrophobicity distribution as well as geometry (the highest approximation to a spherical structure for this fibril). However, this status does not correspond to a micelle-like ordering. Fig. 2.E is a visualisation of the T, O and M distributions of a fibril comprising 24 chains, revealing a significant deviation of the O distribution from the T distribution expressed by a high value of the parameter K = 1.7. The most optimal arrangement for five chains is illustrated by the T, O and M distribution for a five-chain fibril showing, however, characteristics far from micelle-like (Fig. 2.F). The structural specificity of the A-β ‘Osaka’ E22Δ amyloid discussed so far focuses on a proto-fibril form. A similar analysis for a super-fibril system (comprising two proto-fibrils) also reveals a status far from micelle-like ordering (Fig. 3.).

Figure 3: Characterisation of the growing (an increasing number of chains in the fibril) super-fibril of the A-β ‘Osaka’ amyloid with the E22Δ mutation.

A - change in RD (blue) and K (red) for increasing number of chains (horizontal axis). Green line - RD=0.5 level - the threshold adopted to identify a micelle-like system (RD < this level indicates a system with a centric hydrophobic nucleus present together with a polar surface).

B - variation of the sigmaX (blue), SigmaY (red) and SigmaZ (green) parameters with increasing length of the super-fibril.

C - summary of 24 profiles: T (blue), O (red) and M (green) for K=1.7

D - set of profiles: T (blue), O (red) and M (green) for K=0.5. Summary of two chains (from each proto-fibril)

E - 3D form of a super-fibril with 24 chains in each proto-fibril, generated based on the geometry of a 5-chain fibril available in PDB with a single-chain (red) highlighted

F - form of a two-chain super-fibril (with two chains in each proto-fibril) - the length was chosen based on the values of the RD and K parameters closest to the micelle-like arrangement as shown in Fig. 3.A.

The analysis shown in Fig. 3 characterises the structure of the A-β ‘Osaka’ amyloid super-fibril in a way analogous to the presentation of the proto-fibril. The lowest –– yet high –– value of K=0.7 is shown by super-fibrils for 3-11 chains in each proto-fibril. The RD value is above the cut-off level for this set with RD=0.5. This means that, apart from a composition with two chains in each proto-fibril (K=0.5 , RD > 0.6), the most similar characteristics of the superfibril do not qualify the structure to be micelle-like. The complete super-fibril (24 chains in each proto-fibril) reveals a significant deviation of the O distribution from the T distribution, which is typical of A-β group amyloids (Fig. 3.C) [22, 48]. An O distribution most similar to the T distribution is present with a composition of 2 chains in each proto-fibril (Fig. 3.D), albeit this status does not qualify this arrangement as micelle-like. Fig. 3.E is a visualisation of the 3D form of the generated super-fibril comprising 24 chains in each proto-fibril. A single chain (in each proto-fibril) and a two-chain superfibril are shown highlighted (Fig. 3.F). The structure of successive super-fibrils shows values for the interval 3-11 that define the globularity of the structure (expressed by SigmaX, SigmaY and SigmaZ values - Fig. 3.B), yet the RD and K parameter values do not indicate micelle-like structuring of hydrophobicity. To conclude on the characteristics of these two forms of pathological amyloid, the structuring of the amyloid is not adapted to the aquatic environment. As the experiments (the shaking procedure) indicate, a change in ambient (environmental) conditions is required for the amyloid form to be established. The resulting fibril structure adapting to the different environment of polar water (3D Gauss function), treated as an external force field, acquires a fibril form with a high value of the K parameter. According to the interpretation from the FOD-M model, this means that the modified environment (with the external force field expressed by the K parameter value) favours the stabilisation of multi-chain fibrils.

Analysis of functionall fibril – endorphin

Endorphin is defined as a protein representing the function of the reservoir. Endorphin is an example of a hormone stored in the form of a functional amyloid. The release of a single molecule takes place in a cell under the condition of the changing the pH of the environment [51]. This suggests that the polar environment plays a significant role in the function of this hormone. The fibril containing 24 chains was constructed following all symmetry operations present in the 6-chain fibril available in PDB (6TUB) in step-wise procedure. The individual chain as well as chains 2–24 containing fibrils were the objects of analysis. The 3D Gaussian function was generated for individual chains and for all fibrils with an increased number of chains in the fibril. 

Figure 4: Characterisation of the fibril status of the functional amyloid formed by endorphin.

A - summary of the RD (blue) and K (red) values for fibrils with increasing numbers of endorphin chains. Green line - the discrimination level expressed by RD=0.5.

B - variation in the values of the SigmaX (blue), SigmaY (red) and SigmaZ (green) geometrical parameters for an endorphin fibril with an increasing number of chains in the fibril.

C - summary of T (blue), O (red) and M (green) profiles at K=1.3 for a fibril comprising 24 endorphin chains

D - summary of T (blue), O (red) and M (green) profiles for K=0.2 for a fibril of 5 chains

E - fibril endorphin with a 24-chain composition generated from the arrangement present in the available 5-chain fibril (PDB ID - 6TUB).

F - 3D presentation of a single chain and a 5-chain fibril - the forms acceptable to the aquatic environment as representing a micelle-like system.

A functional amyloid like endorphin reveals different characteristics to a pathological amyloid. The single-chain status analysis showed the presence of a micelle-like system with a low K =0.3 and RD well below the discriminating value of RD=0.5 (Fig. 4.A). This set of prameter values indicates a status with very good adaptation to a micelle-like arrangement and therefore a arrangement stabilised by the aquatic environment. A reduction in RD and K values is found for a fibril comprising 2 to 8 chains. K=0.2 indicates an almost perfect adaptation to the micelle-like arrangement. This has important implications for the solubility of such a system both as a single chain and as a fibril with less than nine chains. The fibrils with the composition in question represent a structure adapted to external force field conditions expressed by a 3D Gaussian function. Fibrils longer 8 chains very quickly approach the characteristics of a pathological fibril by a significant increase in the RD and K values. This means that in an aqueous environment, an arrangement of up to 8 chains is acceptable. An increase in the number of chains in the fibril makes the endorphin fibril more akin to the pathological fibril. The aqueous environment does not make a 8+ chain fibril structure acceptable. Otherwise the environment would have to be heavily modified to accept a form that corresponds to a high K value (Fig. 4.A). Fibrils with a composition of 2 to 8 chains represent a globule-like structure (with comparable values of SigmaX, SigmaY and SigmaZ parameters - Fig.4.B). The T, O and M profiles for the 24-chain fibril represent a status comparable to the pathological amyloid, revealing significant differences between the T and O distribution with the M distribution far from the T distribution (Fig. 4.C). A fibril of 5 chains (selected from a set of fibrils with 2 to 8 chains) shows a micelle-like structuring (Fig. 4.D). The structure of the 24-chain fibril formed is shown in Fig. 4.E, revealing a geometrical arrangement typical of endorphin fibrils. A 5-chain structure ilustrates the water-optimised fibril endorphin. (Fig. 4.F).

The characterisation of the fibryl structure of the functional amyloid, endorphin, given above has important implications for the function of this protein. The structure of both the single chain – with functionally disconnected from the fibril – and the limited length of the fibril are proving to be acceptable in the aquatic environment. In contrast, an increase in the number of chains results in a fibril structure requiring an environment different from polar water. The generation of a fibril with an increased number of chains is possible under altered conditions, which are absent in the normal functional environment of this protein. The specificity of the endorphin amyloid in question indicates a naturally encoded form of fibril length termination resulting from conditions imposed by the polar water environment.

Discussion

The feature that makes an amyloid hazardous to the cell is the unrestricted propagation of the amyloid, leading to large arrangement sizes (3.1 (±0.2) nm) and typical lengths in the range 60 to 220 nm, hazardous to the normal functioning of cells and cell organelles [55]. The only way to prevent uncontrolled, unrestricted propagation of the fibril is to terminate it. A natural solution to this problem is also suggested by the analysis of solenoid structures, the theoretically possible propagation of which may result from a similar β structure of plates stabilised by a network of numerous hydrogen bonds. The example of solenoids, which do not form fibrils of unlimited length, reveals a way of stopping such propagation. The terminating factor for solenoid propagation in proteins with this structure turns out to be the helical fragment of the polypeptide chain. The helix is located diagonally in the solenoid clear cross-section, which prevents connection to the next solenoid-type system. An example of such solution is shown in Fig. 5. Based on this system, a therapeutic method was proposed to stop amyloid propagation replicating the mechanism present in solenoids. A drug design method in the form of specific complexation of helical fragments in the lumen of an amyloid fibril was proposed in [56].

Figure 5: 3D presentation (with two orientations) of the solenoids (blue) under construction E.C.4.2.2-pectate lyase (PDB ID - 1JRG [57] with a helix (red) closing the solenoid lumen.

In the pectate lyase example cited here, the status of the entire solenoid is expressed with high RD and K values, while the terminal fragment of the solenoid, together with the helical section, shows a local structuring consistent with a micelle-like arrangement. This results in favourable contact with the water environment and the ability to penetrate it, preventing the attachment of another solenoid from another molecule. It is also clear that the indicated helix geometrically excludes β-plate continuation. This issue is discussed in detail in [58]. Based on the examples of solenoids indicated there, stopping the amyloid propagation by complexing short helices specifically bound to the amyloid fibril was proposed as a drug design [56].

A natural solution to prevent the propagation is indicated by the endorphin structure discussed in this paper. This example reveals the active involvement of the environment in structuring, which prevents fibril propagation to continue in the aquatic environment. Numerous examples [46] have demonstrated the role of the environment, which actively affects the protein folding process in an environmentally dependent manner. Here, it is shown that the environment also affects the structure of multi-chain complexes by limiting the feasibility of their unrestricted attachment. So it is also a form of effect on biological activity. The role of functional amyloids is widely debated, with examples present in the human body as well as other organisms, including insects [59-62]. The application of the FOD-M model to the analysis of the numerous amyloid structures available indicates the importance of environmental effects on amyloid structure formation [63,64].

The introduction of environment influence on folding process requires the changes of models applied for In Silico simulation of this process. The function expressing the energetical status E of protein shall be treated as dependent on two functions:

E = F(r_ij) = F(E_INT(r_ij), E_EXT(K,r_ij))    eq.6.

Where: F(r_ij) expresses the energetical status of folded protein depending on r_ij – distance between interacting atoms, E_INT(r_ij) – internal force field expressing the nonbonding interactions depending on rij and E_EXT(K,r_ij)) – external force field depending on r_ij and K expressing the form of force field as given in eq. 5. The symbol E is to express the physical meaning of the function which expresses the energy status of protein. This problem called in literature multi-object optimisation is searching for consensus between the two contradictory functions. Decrease of E_INT(r_ij) usually causes the increase of E_EXT(K,r_ij)) and vice versa [65]. The procedure solving this problem called front Pareto allows identification of energy minimum (F(r_ij)) for consensus conditions for both functions [65]. This is planned to be applied for simulation In Silico of protein folding process.

Conclusions

The fibrillar form of pathological amyloids is characterised by the unlimited propagation of fibrils destroying the structure of cells. The surprising identification of biologically functional amyloids of typical fibril forms raised a question concerning their differences with respect to pathological ones. It is shown in this paper that the structuralisation depends on the environment. The water surrounding for endorphin fibril accepts the set of chains 2–8 as representing micelle-like organisation that ensures the solubility. The pathological amyloids require changed external conditions as it is shown in A-β “Osaka” mutation. The FOD-M model expresses the specificity of the environment using the K parameter, which expresses the degree of necessary change of the external force field to generate and stabilise the fibril construction. It is also shown that one individual endorphin chain represents the organisation of a micelle-like form ensuring solubility of an individual chain which is released in changed pH conditions, thus suggesting the sensibility to external conditions. The status of one single chain representing micelle-like organisation remains in strong correlation with the biological activity which is accomplished by individual chain. The mathematical model for In Silico protein folding simulation is proposed taking into account the structuralisation of protein as environment conditions dependent.

Data availability

The programming is available in open access system: https://hphob.sano.science.

Acknowledgments

Many thanks to Anna Smietanska and Zdzislaw Wisniowski for technical help. This research was partially supported by the European Union's Horizon 2020 programme under grant Sano No 857533. and Sano project carried out within the International Research Agendas programme of the Foundation for Polish Science. co-financed by the European Union under the European Regional Development Fund.

We gratefully acknowledge Poland's high-performance Infrastructure PLGrid ACK Cyfronet AGH for providing computer facilities and support within computational grant “plgrantfordrippy”.

Author contributions

conceptuation: IR, LK; programming: KS PF, data curation: DD.

Funding and additional

information – Jagiellonian University – Medical College grant# N41/DBS/001127

Conflict of interest

Authors declare: No conflict of interest.

References

1. Loquet A, Saupe SJ, Romero Functional Amyloids in Health and Disease. J Mol Biol 430 (2018): 3629-3630.
2. Siemer What makes functional amyloids work? Crit Rev Biochem Mol Biol 57 (2022): 399-411.
3. Hewetson A, Do HQ, Myers C, et al. Functional Amyloids in Reproduction. Biomolecules 7 (2017): 46.
4. Jackson MP, Hewitt Why are Functional Amyloids Non-Toxic in Humans? Biomolecules 7 (2017): 71.
5. Chiti F, Dobson CM. Protein misfolding, amyloid formation, and human disease: A summary of progress over the last decade. Annu Rev Biochem86 (2017): 27–68.
6. Ross CA, Poirier MA. Protein aggregation and neurodegenerative disease. Nat Med10 (2004): S10–S17.
7. Aguzzi A, O’Connor T. Protein aggregation diseases: pathogenicity and therapeutic perspectives. Nat Rev Drug Discov9 (2010): 237-248.
8. Taylor JP, Hardy J, Fischbeck KH. Toxic proteins in neurodegenerative disease. Science296 (2002):1991-1995.
9. Marshall KE, Vadukul DM, Dahal L, et al. A critical role for the self-assembly of Amyloid-β1-42 in neurodegeneration. Sci Rep 6 (2016): 30182.
10. Yang DS, Serpell LC, Yip CM, et al. Assembly of Alzheimer's amyloid-beta fibrils and approaches for therapeutic intervention. Amyloid 1 (2001): 10-9
11. Romero D, Kolter Functional amyloids in bacteria. Int Microbiol 17 (2014): 65-73.
12. Serpell Amyloid structure. Essays Biochem 56 (2014): 1-10.
13. Hazenberg BP. Amyloidosis: a clinical overview. Rheum Dis Clin North Am 39 (2013): 323-345.
14. Maurer MS, Hanna M, Grogan M, et al. Genotype and Phenotype of Transthyretin Cardiac Amyloidosis: THAOS. (Transthyretin Amyloid Outcome Survey). J Am Coll Cardiol 68 (2016): 161-172.
15. Zibaee S, Fraser G, Jakes R, et al. Human beta-synuclein rendered fibrillogenic by designed mutations. J Biol Chem 285 (2010): 38555-38567.
16. Jain N, Chapman Bacterial functional amyloids: Order from disorder. Biochim Biophys Acta Proteins Proteom 867 (2019): 954-960.
17. Levkovich SA, Gazit E, Bar-Yosef Two Decades of Studying Functional Amyloids in Microorganisms. Trends Microbiol 29 (2021): 251-265.
18. Loquet A, Saupe SJ, Romero Functional Amyloids in Health and Disease. J Mol Biol 430 (2018): 3629-3630.
19. Hewetson A, Do HQ, Myers C, et al. Functional Amyloids in Reproduction. Biomolecules 7 (2017): 46.
20. Ladner-Keay CL, Griffith BJ, Wishart Shaking alone induces de novo conversion of recombinant prion proteins to β-sheet rich oligomers and fibrils. PLoS One 9 (2014): e98753.
21. Riek R. The Three-Dimensional Structures of Amyloids. Cold Spring Harb Perspect Biol 9 (2017): a023572.
22. Roterman I, Stapor K, Dulak D, et al. Secondary structure in polymorphic forms of alpha-synuclein amyloids. Acta Biochim Pol 70 (2023): 435-445.
23. Shuangshuang Zhao, Kuiliang Li, Xiang Sun, et al. Copper-Catalyzed Stereoselective [4 + 2] Cycloaddition of β,γ-Unsaturated α-Keto Esters and 2-Vinylpyrroles in Water. Organic Letters24 (2022): 4224-4228.
24. Ziyuan Li, Cen-Feng Fu, Ziwei Chen, et al. Electron-Induced Synthesis of Dimethyl Ether in the Liquid–Vapor Interface of Methanol. The Journal of Physical Chemistry Letters13 (2022): 5220-5225.
25. Sugimoto Y. Seeing how ice breaks the rule. Science 377 (2022): 264-265.
26. Ben-Amotz Electric buzz in a glass of pure water. Science 376 (2022): 800-801.
27. Chelli R, Pagliai M, Procacci P, et al. Polarization response of water and methanol investigated by a polarizable force field and density functional theory calculations: implications for charge transfer. J Chem Phys 122 (2005): 074504.
28. Mannfors B, Palmo K, Krimm Spectroscopically determined force field for water dimer: physically enhanced treatment of hydrogen bonding in molecular mechanics energy functions. J Phys Chem A 112 (2008): 12667-12678.
29. Pullanchery S, Kulik S, Rehl B, et al. Charge transfer across C-H⋅⋅⋅O hydrogen bonds stabilizes oil droplets in water. Science 374 (2021): 1366-1370.
30. Poli E, Jong KH, Hassanali Charge transfer as a ubiquitous mechanism in determining the negative charge at hydrophobic interfaces. Nat Commun 11 (2020): 901.
31. Marsalek O, Markland Quantum Dynamics and Spectroscopy of Ab Initio Liquid Water: The Interplay of Nuclear and Electronic Quantum Effects. J Phys Chem Lett 8 (2017): 1545-1551.
32. Lee AJ, Rick The effects of charge transfer on the properties of liquid water. J Chem Phys 134 (2011): 184507.
33. Agmon N, Bakker HJ, Campen RK, et al. Protons and Hydroxide Ions in Aqueous Systems. Chem Rev 116 (2016): 7642-7672.
34. Wei Z, Li Y, Cooks RG, et al. Accelerated Reaction Kinetics in Microdroplets: Overview and Recent Developments. Annu Rev Phys Chem 71 (2020): 31-51.
35. Hao H, Leven I, Head-Gordon Can electric fields drive chemistry for an aqueous microdroplet? Nat Commun 13 (2022): 280.
36. Katsuto H, Okamoto R, Sumi T, et al. Ion Size Dependences of the Salting-Out Effect: Reversed Order of Sodium and Lithium Ions. J Phys Chem B 125 (2021): 6296-6305.
37. Chanda A, Fokin Organic Synthesis “On Water”. Chem. Rev 2 (2009): 725–748.
38. Jung Y, Marcus On the nature of organic catalysis "on water". J Am Chem Soc 129 (2007): 5492-5502.
39. Wise PK, Ben-Amotz Interfacial Adsorption of Neutral and Ionic Solutes in a Water Droplet. J Phys Chem B 122 (2018): 3447-3453.
40. Qiu L, Wei Z, Nie H, et al. Reaction Acceleration Promoted by Partial Solvation at the Gas/Solution Interface. Chempluschem 86 (2021): 1362-1365.
41. Bredt AJ, Ben-Amotz Influence of crowding on hydrophobic hydration-shell structure. Phys Chem Chem Phys 22 (2020): 11724-11730.
42. Sugimoto Y. Seeing how ice breaks the rule. Science 377 (2022): 264-265.
43. Ding M, Xu Improving catalysis by moving water. Science 377 (2022): 369-370.
44. Jian Huang, Wei Chen, Jiazhi Liang, et al. α-Keto Acids as Triggers and Partners for the Synthesis of Quinazolinones, Quinoxalinones, Benzooxazinones, and Benzothiazoles in Water. The Journal of Organic Chemistry86 (2021): 14866-14882.
45. Schutzius TM, Jung S, Maitra T, et al. Spontaneous droplet trampolining on rigid superhydrophobic surfaces. Nature 527 (2015): 82-85.
46. Roterman I, Konieczny L. Protein Is an Intelligent Micelle. Entropy (Basel) 25 (2023): 850.
47. Roterman I, Stapor K, Fabian P, et al. Model of Environmental Membrane Field for Transmembrane Proteins. Int J Mol Sci 22 (2021): 3619.
48. Dulak D, Gadzala M, Banach M, et al.Alternative Structures of α-Synuclein. Molecules 25 (2020): 600.
49. Banach M, Konieczny L, Roterman I. The Amyloid as a Ribbon-Like Micelle in Contrast to Spherical Micelles Represented by Globular Proteins. Molecules 24 (2019): 4395.
50. Roterman I, Stapor K, Konieczny L. Structural Specificity of Polymorphic Forms of α-Synuclein Amyloid. Biomedicines 11 (2023): 1324.
51. Seuring C, Verasdonck J, Gath J, et al. The three-dimensional structure of human β-endorphin amyloid fibrils. Nat Struct Mol Biol 27 (2020): 1178-1184.
52. Schütz AK, Vagt T, Huber M, et al. Atomic-resolution three-dimensional structure of amyloid β fibrils bearing the Osaka mutation. Angew Chem Int Ed Engl 54 (2015): 331-335.
53. Levitt MA. A simplified representation of protein conformations for rapid simulation of protein folding. J Mol Biol 104 (1976): 59-107.
54. Kullback S, Leibler RA. On information and sufficiency. Annals Mathemat Statistics 22 (1951): 79-86.
55. Dubnovitsky A, Sandberg A, Rahman MM, et al. Amyloid-β protofibrils: size, morphology and synaptotoxicity of an engineered mimic. PLoS One 8 (2013).
56. Roterman I, Banach M, Konieczny L.Towards the design of anti-amyloid short peptide helices. Bioinformation 14 (2018): 1-7.
57. Thomas LM, Doan CN, Oliver RL, et al. Structure of pectate lyase A: comparison to other isoforms. Acta Crystallogr D Biol Crystallogr 58 (2002): 1008-1015.
58. Banach M, Roterman I. Solenoid – an amyloid under control. In: From globular proteins to amyloids. Editor: Irena Roterman-Konieczna, Elsevier 2020, Amsterdam, Netherlands, Oxford UK, Cambridge MA USA (2020): 95-116.
59. Morris VK, Linser R, Wilde KL, et al. Solid-state NMR spectroscopy of functional amyloid from a fungal hydrophobin: a well-ordered β-sheet core amidst structural heterogeneity. Angewandte Chemie 51 (2012): 12621-12625.
60. Majumdar A, Cesario WC, White-Grindley E, et al. Critical role of amyloid-like oligomers of Drosophila Orb2 in the persistence of memory. Cell 148 (2012): 515-529.
61. Makin OS, Serpell LC. Examining the structure of the mature amyloid fibril. Biochem Soc Trans 30 (2002): 521-525.
62. Brown A, Török Functional amyloids in the human body. Bioorg Med Chem Lett 40 (2021): 127914.
63. Roterman I, Stapor K, Fabian P, et al. In Silico Modeling of the Influence of Environment on Amyloid Folding Using FOD-M Model. Int J Mol Sci 22 (2021): 10587.
64. Roterman I, Stapor K, Gadek K, et al. On the Dependence of Prion and Amyloid Structure on the Folding Environment. Int J Mol Sci 22 (2021): 13494.
65. Kumar K, Kakandikar G, Davim JP. Computational Intelligence in Manufacturing. Woodehead Publishing – Elsevier Ltd. (2022).