1. Introduction

Quantum materials are solid materials which possess unique behaviors that cannot be predicted from the first principles over an extended range of energy and length scales. These properties (such as superconductivity, entanglement, topology, and the Kondo effect) offer interesting pathways towards the production of higher quality products in industries such as computing and energy. Research into material characteristics have revealed that factors responsible for noticeable properties in quantum materials include strong interactions between the electrons present in the material matrix, and a variety of symmetry in the arrangement of matter. The history of quantum materials can be traced to 1957, from the theory of superconductivity which was put forward by researchers John Bardeen, Leon Cooper, and Robert Schrieffer (commonly termed “BCS”). Through this groundbreaking work, the theory of Cooper pair quasiparticles was put forward, which carefully explained the quantum mechanical correlations that exist between electrons. Consequent to the successful explanation of this fundamental quantum material behavior, the condensed matter physical understanding of these materials is currently being understood [1].

Quantum materials can be broadly classified to consist of materials such as:

1. Topological materials: these are materials whose transport behavior is as a result of unique bulk-edge properties. They are mostly s+p electron materials with extended and overlapping orbitals. In more recent materials of this type, partly filled 3d and 4f orbitals are being observed, giving rise to strong Coulombic repulsion. Materials in this category include Bi₂Se₃, WTe₂, Cd₂Se₃, MoTe₂, CeA1Ge and Mn₃
2. Quantum spin liquids (SPLs): these are largely theoretical materials which react antiferromagnetically with nearest neighbors, even at 0K. This material was first introduced by The Nobel Prize winning physicist PW Anderson in early 1970s, and was depicted as frustrated isling spins on a triangle. Examples include the popular Herbertsmithite [ZnCu₃(OH)₆Cl₂], CS₂CuCl₄ and Yb₂Ti₂O₇.
3. Mott Transitions (or Correlated metals): these are certain transition and rare earth metals which act as insulators, due to their unconventional band theory which exist in like character bands (unlike the anionic and cationic state bandgap interactions in charge transfer insulators). Examples of these materials include RTiO₃, RCoO₃, Sr₂RuO₄, Sr₂lrO₄ and CeAl₃.
4. Graphene: these are carbon allotropes which possess Dirac-like dispersions in multiple dimensions (i.e. 1D, 2D or 3D). Its wave electronic behavior and correlation due to bandwidth suppression has been extensively studied by researchers, and this served as a background for the new materials being discovered today.

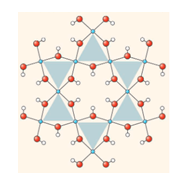
Figure 1: Structure of Herbertsmithite. Reproduced with permission from [2].

1.1. Development and properties of quantum materials

There has been a rapid advancement in the development of quantum materials through the single crystal growth technology. Through this technique, the anisotropies, and defects inherent in these materials are minimized thereby allowing for syntheses based on new forms of quantum magnetism [3-5] and attainment of electronic order in oxides [6]. As a result of these advents, it was discovered that investigations into methods of perfecting the quality of the synthesized crystalline materials would push the frontiers forward. Some of the leading methods that are currently being used for the growth of highly pure quantum material crystals include.

1.2. Chemical vapor transport reactions

This is a complex chemical reaction process that is entailed in the deposition of solid materials at high temperatures of around 1000°C. It can be classified as additive or subtractive, based on the method of component deposition. The general steps involved in these reactions range from a mass transport of gaseous reactants to substrate sites, to the diffusion and adsorption of the reactants followed by surface migration, desorption, diffusion, and transport steps [7]. An advantage of the CVT technique is that the high-quality single crystals generated can be used in the synthesis of critically important products such as Weyl semimetal Ta2Se8l [8] and β-Bi4I4 insulator [9].

1.3. Crucible flux growth

This is a crystallization process that synthesizes intermetallic and oxide materials through a high-temperature melting of inorganic compounds [10]. Candidates for use as inorganic compounds must possess properties such as low melting point, easy separability after crystal growth, lox toxicity and cost, and capability of dissolving a large number of reagents [11]. Examples of materials that have been successfully synthesized using this technique include Bi2Te3, Bi2Ir2O7, R10Mg40Cd50 and Yb14MnSb11 . In instances where the properties of material crystal are to be varied, there is a need to dope with rare-earth elements, with the final material achieving a composition based on the distribution coefficients (K’) calculated as:

Figure 2: (a) Dispersion of energy in the direction of the surface brillouin zones; (b) Observed Fermi-surface for Bi2Se3 sample; (c) Dispersion of energy for Ca-doped sample; (d) Observed Fermi-surface for Ca-doped sample. Reproduced with permission from [19]. Copyright 2012, SST.

1.4. Optical Floating Zone (OFZ) method

This is a light heating technique used in the synthesis of quantum materials in oxygen, argon and air atmospheres and pressures of about 9.5 bar. Through the creation of a molten zone during the synthesis, it is possible to remove material impurities thereby producing semiconductors of extremely high purity [12]. OFZ has proven successful in the study of the ground state and nematic response of ruthenate (Sr₃Ru₂O₇) , which was priorly difficult due to its high disorder rate. Furthermore, OFZ was fundamental in the resolution of the intrinsic magnetic properties of pyrochlore lattices such as titanate and zirconate [13-14]. One of the main challenges in the OFZ synthesis method is the low rate of production of crystal volumes, which is a deterrent to the large scale deployment of the technology. Nonetheless, it remains a fundamental method in the synthesis of complex oxides, with research into the fabrication of high-pressure growth chambers and laser-based heating sources currently underway.

1.5. Czochralski growth method

This is named after Jan Czochralski, a Polish scientist who developed a pulley device that could produce large volume single semiconductor crystals in 1915. This method has been found effective in the synthesis of oxides, fermions, and the novel skyrmion materials [15]. In using this method in the synthesis of quantum materials, the arc-melting furnace and radio-frequency (RF)-induction heating techniques. An outstanding ability of the Czochralski technique with regards to quantum material synthesis is in the analysis of low-temperature properties of compounds. Examples of these properties include the Fermi-surface determination of FeSi semiconductor, and quantum Hall effects in the antiferromagnetic phase of Mn₃Sn compound. However, considerable research is still needed in the improvement of crystal quality due to component or compound volatility. Intriguing physical phenomena are very diversified in quantum materials, and they depend on the electron and atomic behaviors in these materials. These behaviors are often observed during experimental procedures through the use of state-of-the-art instruments. Examples include:

2. Superconductivity

Superconductivity, put simply, is the ability of some materials to transmit direct current at temperatures below a critical point (referred to as Tc) with little or no loss in energy. With respect to the study of quantum materials, the superconductivity is the mostly widely researched many-body phenomenon after being discovered by Heike Onnes in 1911. The concept behind this was explained in 1957, and it has been established to be as a result of the formation of formation of electrons pairs by negative electrons at temperatures below Tc due to strong atomic-level vibrations (phonons). Specifically, with respect to quantum materials, the superconductivity in cuprates, ruthenates and antiferromagnetic materials (such as BaFe₂As₂) is undergoing intense research. Important explanations are being sought concerning the light-induced motions observed in cuprates as well as coupling interactions in AFM materials at high Tc [16-17].

2.1. Topological phases

Topological quantum materials (such as superfluids and insulators) depends heavily on the classification of materials based on observed shapes during continuous deformation. Through the use of time-reversal and symmetrical techniques, it is possible to get more information on these materials based on inherent crystalline structures. Towards further understanding the effect of structure on observed material behavior, single-particle band structure calculations and advances in experimental synthesis have proven instrumental. An example of such experimental approach is the Angle-Resolved Photoemission Spectroscopy (ARPES), which is being used to understand how electronic-scale interactions could help account for the changes in band dispersions and quasiparticle lifetimes that are observed [18]. Figure 2 below portrays the use of this technology in the understanding of the structure of Bi₂Se₃ through the use of a pump emitting photons of energy into electrons in the material thereby revealing inherent quantized conduction band states.

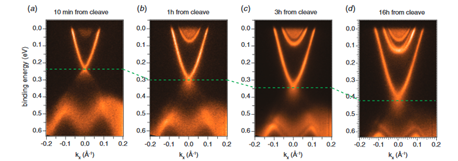
Figure 2: (a) Dispersion of energy in the direction of the surface brillouin zones; (b) Observed Fermi-surface for Bi2Se3 sample; (c) Dispersion of energy for Ca-doped sample; (d) Observed Fermi-surface for Ca-doped sample. Reproduced with permission from [19]. Copyright 2012, SST.

Apart from Flux Quantization depicted above, another topological quantum phenomena that has been immensely studied is the Quantum Hall Effect. This is the adoption of quantized values by 2D electron systems as a result of ‘quantum Hall transitions” observed in conductance (5). The quantized Hall resistance (RQH), pertinent to this phenomena can be expressed according to [20], as:

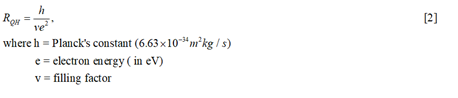
Apart from the possibility of non-magnetic ternary compounds through theoretic predictions of dirac states configurations around the Fermi level, it is now possible to synthesize novel topological insulators such as EuSn₂P₂ [21].

2.2. X-ray studies of Quantum materials

X-radiations are innovative approaches used to understand the structure of quantum materials through the incidence of photons (around 10pm to 10nm). The properties of interest when using this approach include bandwidth, average polarization, coherence length and flux. The energies and wavelength can then be used to deduce the atomic energy levels and size of unit cells. The energy resolution obtained using X-rays is constrained by the large bandwidth of this approach. Apart from this, there is the constant challenge of source stability, thereby requiring the design of novel X-ray scattering approaches. By combining X-Ray Reflectivity (RXR) with multiplet ligand field theory (MLFT) approaches, it is possible to get more insight into correlated insulators, reconstructed interfaces, and staggered moments in ordered materials [22]. The use of Free-Element Laser (FEL) has helped to address the energy and instability challenges through the production of pulses with narrower bandwidth [23], while ultrafast resonant inelastic X-ray scattering is effective in the analysis of structure of light sensitive quantum materials [24].

2.3. Nanoscale quantum materials

The integration of nanotechnology in the synthesis of quantum materials is receiving much attention within the scientific community. This is due to the possibility of engineering the band structure through nanoscale confinement and the improvement of the surface area and defect properties. The energy level correlation with the nanoscale size is presented in the Appendix, and it clearly shows the inverse proportionality relationship. Chemical vapor deposition and additive synthesis are the two major methods used in the synthesis of 2D materials, and phase transitions through intercalative processes have been found to impact hydrogen evolution reaction (HER) for energy generation. The configuration of the morphological properties in quantum materials through the use of disordered materials are currently being assessed, and these are termed amorphous quantum materials. This phenomenon becomes evident at theoretical widths of 5A°, with an expected reduction in the tail states expected if this dimension remains constant. The variation in the composition of amorphous silica using spin-orbit coupling was used to detect clinical translation effects in the resulting materials, which was found to depend on the delocalization of inherent π- electron dye systems [25].

2.4. Advances in quantum material synthesis

The success of emerging areas such as quantum computing depends on the ability to devise novel methods for manipulating and tuning quantum materials, thereby leading to better information retrieval and processing with negligible energy losses. This would require innovations in quantum order-breaking fluctuations which would help to generate materials that are extremely resistant to external perturbations. Significant progresses are also being made in the semiconductor industry, where innovations in materials such as topological insulators, Weyl and Dirac semimetals are gaining momentum. In moving from conventional semiconductors to these new classes of materials, improvements are made on the bulk band structural characterization. Topological crystalline insulators (TCI) are devices in which topological (Dirac) surface states surround high symmetry facets present within the material. Examples of material classes where this behavior is being noticed on their [111], [110] and [100] planar surfaces include Pb_1-xSn_xTe and Pb_1-xSn_xSe [26,27]. Figure 3 presents the energy band evolution that occurs in this class of novel materials.

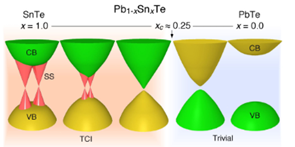
Figure 3: Representation of nontrivial electronic topology in Pb_1-xSn_xTe materials. Reproduced with permission from [26]. Copyright 2013, PR.

As seen above, the material behaves as a Dirac semimetal at compositions above 0.25, while trivial topological transitions are witnessed beyond the critical region. Another aspect of quantum material synthesis currently experiencing rapid advances is in the static perturbation of 2D materials through the process of hetero-structuring. As a result of this, ballistic transport limits which have been exceeded in previous designs are being integrated in the electric conductance of novel van der waals materials such as graphene [28]. The discovery of new materials with inherent quantum mechanical properties are always welcome, especially in quantum spin liquids (QSLs). An example of such material is the recently developed hexagonal perovskite material. It has been discovered that by being synthesized in the form of an oxide, the face-sharing of octahedral or trigonal prism frameworks becomes possible thereby mimicking the metal-metal and metal-oxygen-metal bond angles in conventional perovskites [29]. Hexagonal perovskites are particularly preferred to the conventional cubic perovskites due to the wide variability in their crystal structures. The critical importance of QSLs in neutron scattering advances have led to the evaluation of hexagonal perovskites as possible candidates, due to its possibility of being synthesized as single crystals using optical floating zone methodology. Some materials that have been identified include Ba₄NbIr₃O₁₂, BaY₂Rh₂Ti₂O₁₇ and Ba₃CoSb₂O₉.

3. Challenges

Despite the tremendous progress that has been made in the synthesis of quantum materials for application in critical industries, some scientific challenges need to be addressed in order to improve the efficiency of these materials:

1. There is a need for more control in the observed order and disorder within these materials. A common problem currently being observed is the partial melting of ordered electronic states during quantum phase transitions. This behavior has been detected in nematic liquid crystal phases, and also in high temperature superconductors. Some critical questions that need to be answered is if this partial melting is as a result of inherent disorders, does it result in the development of a new order within the material matrix, and how can it be optimized for material property efficiency.
2. How can changes in the Chern number (number of electronic energy bands) as a result of topological phase transitions be addressed in QSLs. This would affect the rate at which these materials can be integrated into decoherence-resistant quantum computing advances. To solve this, insights into the presence of new metallic states within these materials would help to provide possible correlations between singlet spin pairs and charge introduction thereby assessing the efficacy of P.W. Anderson’s Resonating Valence Bond (RVB) theories in these materials [30].
3. There is also a need to understand more comprehensively the mechanism on non-BCS superconductivity. This would help to assess whether there are changes in the aspects of multiband superconductivity observed in iron-based pnictides and chalcogenides during material doping or application of external pressure.

References

1. Keimer B, Moore JE. The physics of quantum materials. Nature Physics 13 (2017): 1045-1055.
2. Lee PA. An end to the drought of quantum spin liquids. Science 321 (2008): 1306-1307.
3. Lester C, Silvia Ramos RS, Perry TP, et al. Field-tunable spin-density-wave phases in Sr 3 Ru 2 O 7. Nature materials14 (2015): 373-378.
4. Kim C, Matsuura AY, Shen Z-X, et al. Observation of spin-charge separation in one-dimensional srcu o 2." Physical review letters 77 (1996): 4054.
5. Ross Kate A, Lucile Savary, Bruce D. Gaulin, and Leon Balents. Quantum excitations in quantum spin ice. Physical Review X 1 (2011): 021002.
6. Tokunaga, Yusuke, Thomas Lottermoser, et al. Rotation of orbital stripes and the consequent charge-polarized state in bilayer manganites." Nature materials 5 (2006): 937-941.
7. Yan, Xiu-Tian, Yongdong Xu. Chemical vapour deposition: an integrated engineering design for advanced materials. Springer Science & Business Media (2010).
8. Gooth J, Bradlyn B, Honnali S, et al.Axionic charge-density wave in the Weyl semimetal (TaSe 4) 2 I." Nature 575 (2019): 315-319.
9. Bostwick, Aaron, Marco Grioni, et al. A novel quasi-one-dimensional topological insulator in bismuth iodide β-Bi 4I4. Nature Materials 15 (2016): 154-1558"
10. Elwell, Dennis, Hans J, et al. "Crystal growth from high temperature solutions." Journal of The Electrochemical Society 123 (1976): 319.
11. Bugaris, Daniel E, Hans-Conrad zur Loye. Materials discovery by flux crystal growth: quaternary and higher order oxides. Angewandte chemie international edition 51 (2012): 3780-3811.
12. Schmehr, Julian L, Stephen D, et al. Active crystal growth techniques for quantum materials." Annual Review of Materials Research 47 (2017): 153-174.
13. Gardner JS, BD Gaulin, D McK Paul. Single crystal growth by the floating-zone method of a geometrically frustrated pyrochlore antiferromagnet, Tb2Ti2O7. Journal of crystal growth 191 (1998): 740-745.
14. Kimura, Kenta, S Nakatsuji, et al. Quantum fluctuations in spin-ice-like Pr 2 Zr 2 O 7. Nature communications 4 (2013): 1-6.
15. Oike, Hiroshi, Akiko Kikkawa, et al. Interplay between topological and thermodynamic stability in a metastable magnetic skyrmion lattice." Nature Physics 12 (2016): 62-66.
16. Först M, RI Tobey, H Bromberger, et al. Melting of charge stripes in vibrationally driven La 1.875 Ba 0.125 CuO 4: Assessing the respective roles of electronic and lattice order in frustrated superconductors. Physical review letters 112 (2014): 157002.
17. Yang LX, G Rohde, T Rohwer, et al. Ultrafast modulation of the chemical potential in BaFe 2 As 2 by coherent phonons. Physical Review Letters 112 (2014): 207001.
18. Samarth Nitin. Quantum materials discovery from a synthesis perspective." Nature materials 16 (2017): 1068-1076.
19. Bianchi, Marco, Richard C, et al "The electronic structure of clean and adsorbate-covered Bi2Se3: an angle-resolved photoemission study." Semiconductor Science and Technology 27 (2012): 124001.
20. Callegaro, Luca, Vincenzo D'Elia, et al. Realization of the farad from the dc quantum Hall effect with digitally assisted impedance bridges. Metrologia 47 (2010): 464.
21. Gui, Xin, Ivo Pletikosic, et al. "A New Magnetic Topological Quantum Material Candidate by Design." ACS central science 5 (2019): 900-910.
22. Fürsich, Katrin, Volodymyr B, et al. Theory-restricted resonant x-ray reflectometry of quantum materials. Physical Review B 97 (2018): 165126.
23. Buzzi, Michele, Michael Först, et al. Probing dynamics in quantum materials with femtosecond X-rays." Nature Reviews Materials 3 (2018): 299-311.
24. Mitrano, Matteo, Yao Wang. Probing light-driven quantum materials with ultrafast resonant inelastic X-ray scattering." Communications Physics 3 (2020): 1-9.
25. Kohle, Ferdinand FE, Joshua A, et al. Amorphous quantum nanomaterials." Advanced Materials 31 (2019): 1806993.
26. Tanaka Y, T Sato, K Nakayama, et al. Tunability of the k-space location of the Dirac cones in the topological crystalline insulator Pb 1− x Sn x Te. Physical Review B 87 (2013): 155105.
27. Liang, Tian, Quinn Gibson, et al. Evidence for massive bulk Dirac fermions in Pb 1− x Sn x Se from Nernst and thermopower experiments. Nature communications 4 (2013): 1-9.
28. Novoselov KS, OA Mishchenko, et al. 2D materials and van der Waals heterostructures." Science 353 (2016).
29. Nguyen, Loi T, RJ Cava. Hexagonal Perovskites as Quantum Materials." arXiv preprint arXiv (2006): 05864.
30. Anderson, Philip W. The resonating valence bond state in La2CuO4 and superconductivity. Science 235 (1987): 1196-1198